Cliquer ici pour modifier.
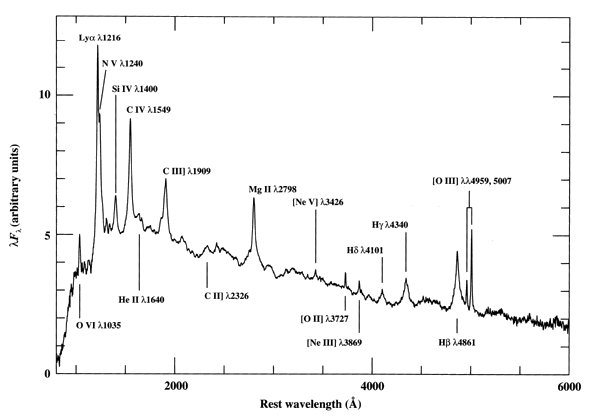
A mean QSO spectrum formed by averaging spectra of over 700 QSOs from the Large Bright Quasar Survey. Prominent emission lines are indicated. Data courtesy of P. J. Francis and C. B. Foltz.
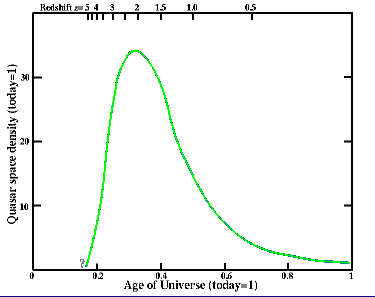
Number of quasars, showing a peak 12 billion years ago.
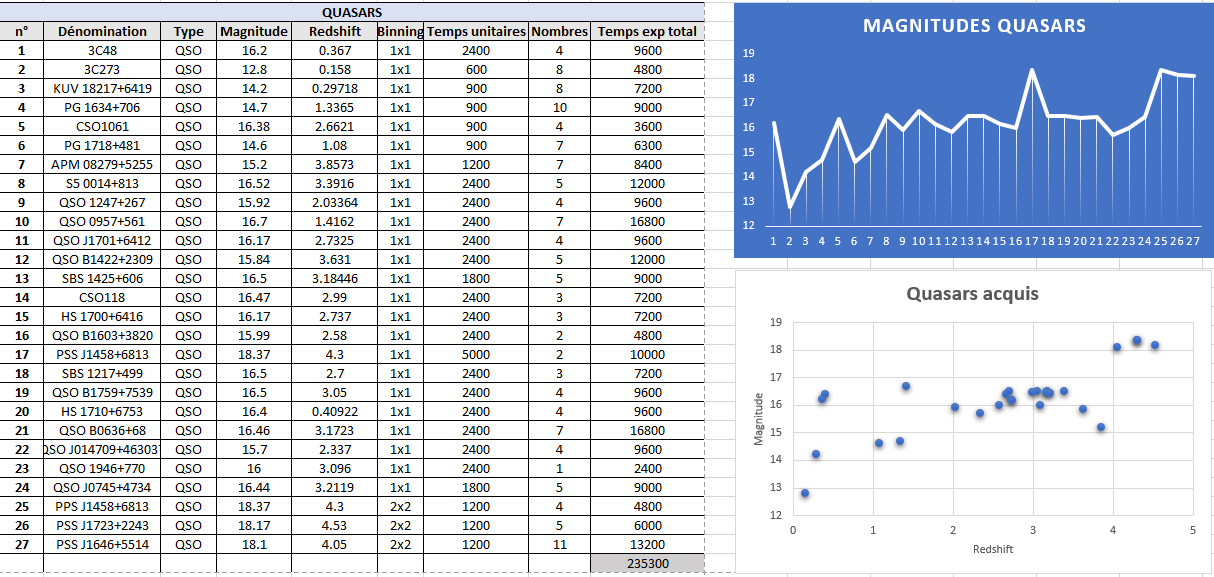
Liste des Quasars acquis :
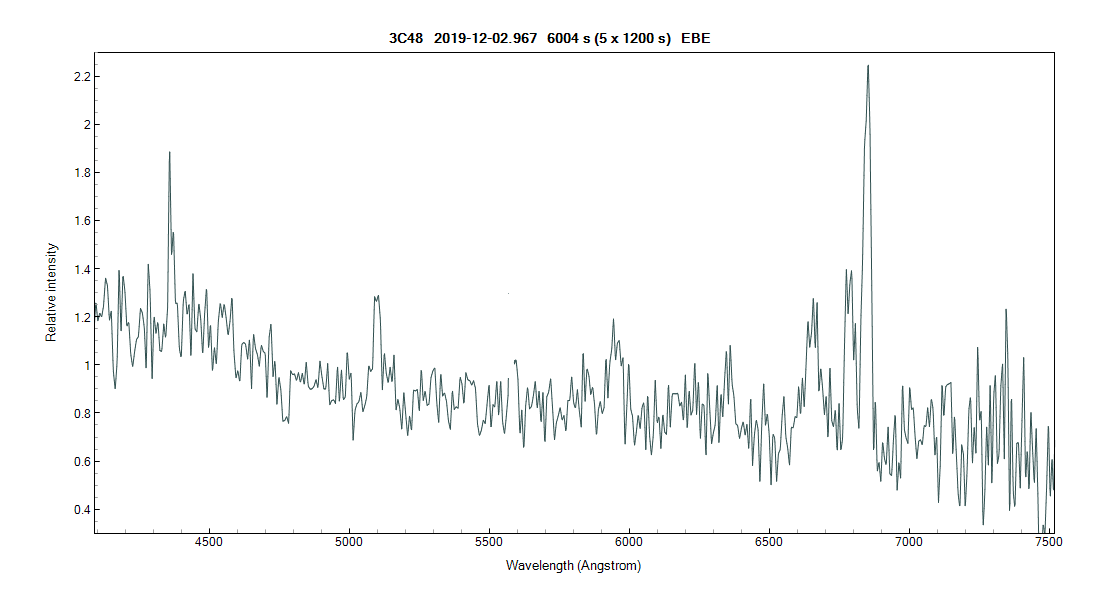
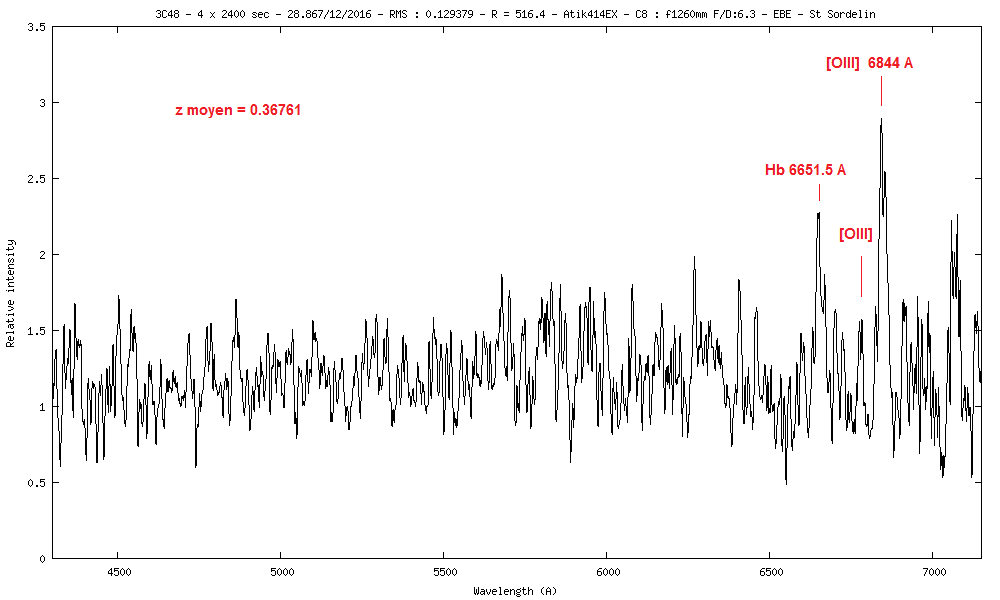
1) 3C48 m=16.2 z=0.367
3C 48 est la première source radio quasi-stellaire (quasar) du Third Cambridge Catalogue of Radio Sources (3C) pour laquelle une identification optique par interférométrie a été obtenue dans les années 1960 par Allan Sandage et Thomas Matthews.
"Cela en ferait le premier quasar découvert", bien que sa confirmation tardive fait qu'il se dispute ce rang avec 3C 273.
Au début des années 1960, Allan Sandage et Thomas Matthews identifient 3C 48. Avec Jesse Greenstein, Matthews obtient pour l'objet un décalage vers le rouge de 0,367, ce qui en fait l'un des décalages les plus élevés de l'époque.
Ce n'est cependant pas avant 1982 que la nature de 3C 48 est confirmée par l'observation des « nébulosités » l'entourant.
"Cela en ferait le premier quasar découvert", bien que sa confirmation tardive fait qu'il se dispute ce rang avec 3C 273.
Au début des années 1960, Allan Sandage et Thomas Matthews identifient 3C 48. Avec Jesse Greenstein, Matthews obtient pour l'objet un décalage vers le rouge de 0,367, ce qui en fait l'un des décalages les plus élevés de l'époque.
Ce n'est cependant pas avant 1982 que la nature de 3C 48 est confirmée par l'observation des « nébulosités » l'entourant.
| _3c48_20161228_811_ebe.fit | |
| File Size: | 40 kb |
| File Type: | fit |
| _3c48_20191202_967_ebe.fit | |
| File Size: | 14 kb |
| File Type: | fit |
1) Avec ces deux raies (Hb et [OIII], je trouve un z moyen = 0.36761
2) Le redshift (z) permet de calculer la vitesse de recession :
Calcul de la vitesse de récession relativiste :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792,458 x [((0,367 + 1)^2 - 1) / ((0,367 + 1)^2 + 1)]
Vr = 299792,458 x (0,86869 / 2,86869
Vr = 299792,458 x 0,30281
Vr = 90 782,4 km/s
3) On peut aussi calculer sa distance ; même si la loi ne marche plus trop pour les longues distances :
D = v / H0 (avec D en Mpc, v en km/s, et H0 en km/s/Mpc
D = 90 782,4 / 70
D = 1 296.9 Mpc soit 4,22 milliards d'années lumières.
4) Calcul de la vitesse grâce à la largeur des raies Hb et [OIII] :
Sur Hb je trouve V= (30/4861) x 299792.458
V= 1850 km/s
Sur [OIII] V = (30/5007) x 299792.458
V = 1796 km/s
2) Le redshift (z) permet de calculer la vitesse de recession :
Calcul de la vitesse de récession relativiste :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792,458 x [((0,367 + 1)^2 - 1) / ((0,367 + 1)^2 + 1)]
Vr = 299792,458 x (0,86869 / 2,86869
Vr = 299792,458 x 0,30281
Vr = 90 782,4 km/s
3) On peut aussi calculer sa distance ; même si la loi ne marche plus trop pour les longues distances :
D = v / H0 (avec D en Mpc, v en km/s, et H0 en km/s/Mpc
D = 90 782,4 / 70
D = 1 296.9 Mpc soit 4,22 milliards d'années lumières.
4) Calcul de la vitesse grâce à la largeur des raies Hb et [OIII] :
Sur Hb je trouve V= (30/4861) x 299792.458
V= 1850 km/s
Sur [OIII] V = (30/5007) x 299792.458
V = 1796 km/s
2) 3C273 m=12.8 z=0.158
3C 273 est un quasar situé dans la constellation Zodiacale de la Vierge. C'est le quasar le plus brillant du ciel,
avec une magnitude apparente de +12,9, et l'un des plus proches, son décalage vers le rouge valant 0,158.
A noter, que la magnitude de Véga étant à peu près 0 et celle du quasar de 12,9 celui-ci est 100 000 moins lumineux.
Sa distance de luminosité est 2,44 milliards d'année-lumières. Ce quasar est l'un des objets les plus lumineux du ciel, avec une magnitude absolue (M) égale à -26,7 déduite grâce au module de distance.
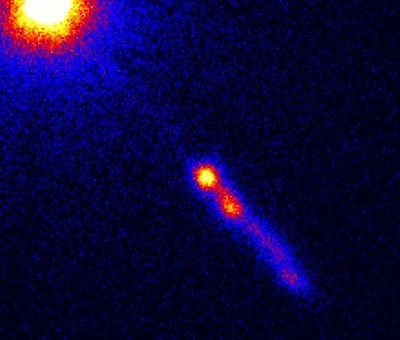
Sa masse a été mesurée grâce à la technique de cartographie de réverbération, et est estimée à 887±187 millions de masses solaires. Un jet est clairement visible sur les images du quasar, et s'étend sur environ 67 kpc. Il a été observé par le télescope spatial Hubble une première fois le 4 juin 1994 pendant 30 minutes de pose, puis une seconde fois entre le 19 et le 20 juillet 2002 pendant 4 heures de pose où le coronographe ACS
(Advanced Camera for Survey) en a révélé les nombreux détails.
Histoire :
Son nom signifie que cet objet est le 273ème objet du troisième catalogue de Cambridge recensant les sources radio. Les coordonnées précises de l'objet ont été déterminées par Cyril Hazard au radio télescope de l'Observatoire de Parkes, à l'occasion d'une occultation par la Lune, et très vite sa contrepartie optique a pu être observée. En 1963,Maarten Schmidt et Bev Oke ont publié un article dans la revue Nature expliquant que 3C 273 était un objet extrêmement lointain, avec un décalage vers le rouge le plaçant à plusieurs milliards d'années-lumière.
Avant cette découverte, beaucoup d'autres sources radio avaient été associées à une contrepartie optique, le premier d'entre eux étant 3C 48.
avec une magnitude apparente de +12,9, et l'un des plus proches, son décalage vers le rouge valant 0,158.
A noter, que la magnitude de Véga étant à peu près 0 et celle du quasar de 12,9 celui-ci est 100 000 moins lumineux.
Sa distance de luminosité est 2,44 milliards d'année-lumières. Ce quasar est l'un des objets les plus lumineux du ciel, avec une magnitude absolue (M) égale à -26,7 déduite grâce au module de distance.
Sa masse a été mesurée grâce à la technique de cartographie de réverbération, et est estimée à 887±187 millions de masses solaires. Un jet est clairement visible sur les images du quasar, et s'étend sur environ 67 kpc. Il a été observé par le télescope spatial Hubble une première fois le 4 juin 1994 pendant 30 minutes de pose, puis une seconde fois entre le 19 et le 20 juillet 2002 pendant 4 heures de pose où le coronographe ACS
(Advanced Camera for Survey) en a révélé les nombreux détails.
Histoire :
Son nom signifie que cet objet est le 273ème objet du troisième catalogue de Cambridge recensant les sources radio. Les coordonnées précises de l'objet ont été déterminées par Cyril Hazard au radio télescope de l'Observatoire de Parkes, à l'occasion d'une occultation par la Lune, et très vite sa contrepartie optique a pu être observée. En 1963,Maarten Schmidt et Bev Oke ont publié un article dans la revue Nature expliquant que 3C 273 était un objet extrêmement lointain, avec un décalage vers le rouge le plaçant à plusieurs milliards d'années-lumière.
Avant cette découverte, beaucoup d'autres sources radio avaient été associées à une contrepartie optique, le premier d'entre eux étant 3C 48.
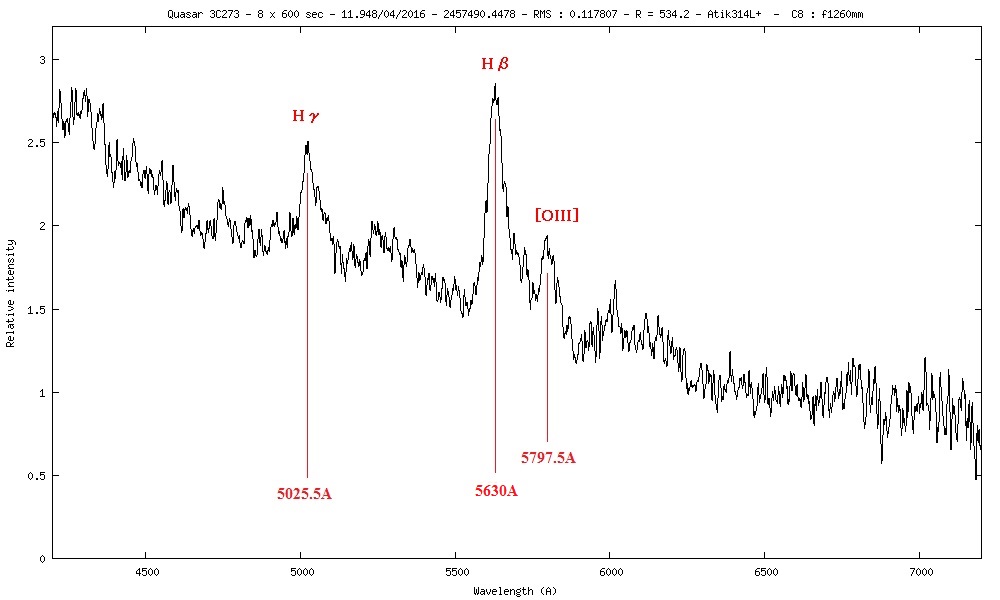
Spectre 1D du Quasar 3C273 traité avec ISIS.
| 3c273_quasar.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Cet objet est donc si lointain, que l'on observe un décalage spectral sur les raies d'émission qui sont décalées vers le rouge, l'objet s'éloignant. C'est tout le spectre qui se retrouve décalé dans les grandes longueurs d'ondes.
La raie Hα n’apparaît plus dans le spectre, car décalée vers 7600Å.
La raie Hβ elle est bien présente précisement à 5629,5Å au lieu des 4861,33Å en laboratoire.
Par ces informations toutes simples (les décalages des raies) et les lois de la lumière on peut tirer un quantité d'informations :
1) Calcul du décalage vers le rouge: redshift (z) :
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = ((5629,5 – 4861,33) / 4861,33
z = 0.158
2) Le redshift (z) permet de calculer la vitesse d'éloignement :
Calcul de la vitesse de récession relativiste :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((0,158 + 1)^2 - 1) / ((0,158 + 1)^2 + 1)]
Vr = 299792.458 x (0,340964 / 2,340964)
Vr = 299792.458 x 0,145651
Vr = 43 665,1 km.s-1
3) On peut aussi calculer sa distance ; par la loi qui relie vitesse, distance, et loi de Hubble :
D = v / H0 (avec D en Mpc, v en km.s-1, et H0 en km.s-1.Mpc-1 : à noter que la constante de Hubble est connue avec une marge d’erreur de +/- 10%).
D = 43 665.1 / 70
D = 623.78 Mpc
4) Sachant qu'un Mpc équivaut à 3.26 x 106 AL, on trouve que le quasar 3C273 est à une distance en années lumières :
D = 623.78 x (3.26 x 10^6)
D = 2.03 x 10^9 AL (AL = années lumières)
Notre quasar est à 2.03 milliards d'années lumières. (Pour rappel le Big Bang a eu lieu il y a 13.7 milliards d'années. La distance avec la galaxie M31 est de 2.54 millions d'années lumières, il faudrait 1004 fois cette distance pour arriver à ce quasar...)
5) On va convertir cette distance d'années lumières en Km :
1 AL = 9.45 x 10^12 km
donc (2.03 x 10^9) x (9.45 x 10^12) = 1.91 x 10^22 km.
Le quasar est à 1.91x 10^22 km.
6) De part sa grande distance on aussi peut déduire des paramètres cosmologiques :
(source documetaire : Astronomie et astrophysiques d'Agnès Acker)
Pour un photon Hβ 4861Å observé à 5629,5Å, le facteur d'étirement est égal à (5629,5/4861.33) = 1.158
Donc le facteur d’échelle au moment de l'émission était de :
a(t) = 1/1.158
a(t) = 0.8635.
Le facteur d'échelle se calcule aussi par la formule :
a(t) = 1 / (1+z)
ou a(t) = 1 / (1 + 0,158)
a(t) = 0.8635
(à noter que le redshift se calcule aussi par la formule : z = (1 - a(t)) / a(t)
L'univers s'est agrandi de 15.8% depuis l'émission des photons jusqu'à cette réception.
Que valait la distance de ce quasar Q au moment de l'émission ? L'expansion a éloigné le quasar Q de l'observateur O, d'autant plus que le temps de voyage de la lumière était plus long. On peut calculer que la distance D1 de Q(t1) à O(t0) est telle que :
D1 = 3 x τa (1-√a) (avec τ =14 milliards d'années) ce qui correspond à une valeur de :
D1 = 3 x 14 x 0,8635 x (1-√0.8635)
D1 = 2,566 milliards d'années lumières.
Cette distance a été étirée d'un facteur (1/a) donc maintenant le quasar Q se trouve à
D0 = 42 x (1-√a)
D0 = 42 x (1-√0.8635)
D0 = 2,971 milliards d'années.
Donc un photon émis au temps t1 par ce quasar sera reçu 2,56 milliards d'années plus tard, quand sa distance sera de 2,97 milliards d'année-lumières (valeurs correspondant au temps de voyage de la lumière).
7) On peut aussi calculer son Flux (ƒ)
(source documetaire : Mooc astrophysique ANU-ASTRO1X (Greatest Unsolved Mysteries of the Univers))
ƒ = L / (4π x D^2 x (1 + z)^2 )
(ƒ est le flux watts par mètres carrés (W.m-2) , D est la distance en mètres (m), L est la luminosité en Watts (W), et z le redshift).
- Sachant que le quasar 3C273 a une luminosité de 10^12 luminosités solaire, ce qui correspond à 100 fois la luminosité de notre galaxie, la luminosité solaire étant de 3,9 x 10^26W.
- La luminosité du quasar 3C273 = 3,9 x 10^38W
- La distance trouvée étant de 623.78Mpc, cela nous donne une distance de 1.91 x 10^25m.
- Le redshift est de 0,158.
ƒ = L / (4π x D^2 x (1 + z)^2 )
ƒ = 3,9 x 10^38 / (4π x ((1.91 x 10^25)^2 ) x (1+0,158)^2)
ƒ = 3,9 x 10^38 / (6.14 x 10^51)
ƒ = 6.34 x 10^14W.m^-2
Le flux reçu du quasar 3C273 est de 6.34 x 10^-14W.m-2
8) On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift :
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = (2,725 x (1 + 0,158)) / (1+0)
T(t1) = 3,155 K
(documents du cours de Cosmologie de Mr Valls-Gabaub 12/04/2016)
Quand les photons sont parties l'Univers avait une température de 3,155 K
La raie Hα n’apparaît plus dans le spectre, car décalée vers 7600Å.
La raie Hβ elle est bien présente précisement à 5629,5Å au lieu des 4861,33Å en laboratoire.
Par ces informations toutes simples (les décalages des raies) et les lois de la lumière on peut tirer un quantité d'informations :
1) Calcul du décalage vers le rouge: redshift (z) :
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = ((5629,5 – 4861,33) / 4861,33
z = 0.158
2) Le redshift (z) permet de calculer la vitesse d'éloignement :
Calcul de la vitesse de récession relativiste :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((0,158 + 1)^2 - 1) / ((0,158 + 1)^2 + 1)]
Vr = 299792.458 x (0,340964 / 2,340964)
Vr = 299792.458 x 0,145651
Vr = 43 665,1 km.s-1
3) On peut aussi calculer sa distance ; par la loi qui relie vitesse, distance, et loi de Hubble :
D = v / H0 (avec D en Mpc, v en km.s-1, et H0 en km.s-1.Mpc-1 : à noter que la constante de Hubble est connue avec une marge d’erreur de +/- 10%).
D = 43 665.1 / 70
D = 623.78 Mpc
4) Sachant qu'un Mpc équivaut à 3.26 x 106 AL, on trouve que le quasar 3C273 est à une distance en années lumières :
D = 623.78 x (3.26 x 10^6)
D = 2.03 x 10^9 AL (AL = années lumières)
Notre quasar est à 2.03 milliards d'années lumières. (Pour rappel le Big Bang a eu lieu il y a 13.7 milliards d'années. La distance avec la galaxie M31 est de 2.54 millions d'années lumières, il faudrait 1004 fois cette distance pour arriver à ce quasar...)
5) On va convertir cette distance d'années lumières en Km :
1 AL = 9.45 x 10^12 km
donc (2.03 x 10^9) x (9.45 x 10^12) = 1.91 x 10^22 km.
Le quasar est à 1.91x 10^22 km.
6) De part sa grande distance on aussi peut déduire des paramètres cosmologiques :
(source documetaire : Astronomie et astrophysiques d'Agnès Acker)
Pour un photon Hβ 4861Å observé à 5629,5Å, le facteur d'étirement est égal à (5629,5/4861.33) = 1.158
Donc le facteur d’échelle au moment de l'émission était de :
a(t) = 1/1.158
a(t) = 0.8635.
Le facteur d'échelle se calcule aussi par la formule :
a(t) = 1 / (1+z)
ou a(t) = 1 / (1 + 0,158)
a(t) = 0.8635
(à noter que le redshift se calcule aussi par la formule : z = (1 - a(t)) / a(t)
L'univers s'est agrandi de 15.8% depuis l'émission des photons jusqu'à cette réception.
Que valait la distance de ce quasar Q au moment de l'émission ? L'expansion a éloigné le quasar Q de l'observateur O, d'autant plus que le temps de voyage de la lumière était plus long. On peut calculer que la distance D1 de Q(t1) à O(t0) est telle que :
D1 = 3 x τa (1-√a) (avec τ =14 milliards d'années) ce qui correspond à une valeur de :
D1 = 3 x 14 x 0,8635 x (1-√0.8635)
D1 = 2,566 milliards d'années lumières.
Cette distance a été étirée d'un facteur (1/a) donc maintenant le quasar Q se trouve à
D0 = 42 x (1-√a)
D0 = 42 x (1-√0.8635)
D0 = 2,971 milliards d'années.
Donc un photon émis au temps t1 par ce quasar sera reçu 2,56 milliards d'années plus tard, quand sa distance sera de 2,97 milliards d'année-lumières (valeurs correspondant au temps de voyage de la lumière).
7) On peut aussi calculer son Flux (ƒ)
(source documetaire : Mooc astrophysique ANU-ASTRO1X (Greatest Unsolved Mysteries of the Univers))
ƒ = L / (4π x D^2 x (1 + z)^2 )
(ƒ est le flux watts par mètres carrés (W.m-2) , D est la distance en mètres (m), L est la luminosité en Watts (W), et z le redshift).
- Sachant que le quasar 3C273 a une luminosité de 10^12 luminosités solaire, ce qui correspond à 100 fois la luminosité de notre galaxie, la luminosité solaire étant de 3,9 x 10^26W.
- La luminosité du quasar 3C273 = 3,9 x 10^38W
- La distance trouvée étant de 623.78Mpc, cela nous donne une distance de 1.91 x 10^25m.
- Le redshift est de 0,158.
ƒ = L / (4π x D^2 x (1 + z)^2 )
ƒ = 3,9 x 10^38 / (4π x ((1.91 x 10^25)^2 ) x (1+0,158)^2)
ƒ = 3,9 x 10^38 / (6.14 x 10^51)
ƒ = 6.34 x 10^14W.m^-2
Le flux reçu du quasar 3C273 est de 6.34 x 10^-14W.m-2
8) On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift :
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = (2,725 x (1 + 0,158)) / (1+0)
T(t1) = 3,155 K
(documents du cours de Cosmologie de Mr Valls-Gabaub 12/04/2016)
Quand les photons sont parties l'Univers avait une température de 3,155 K
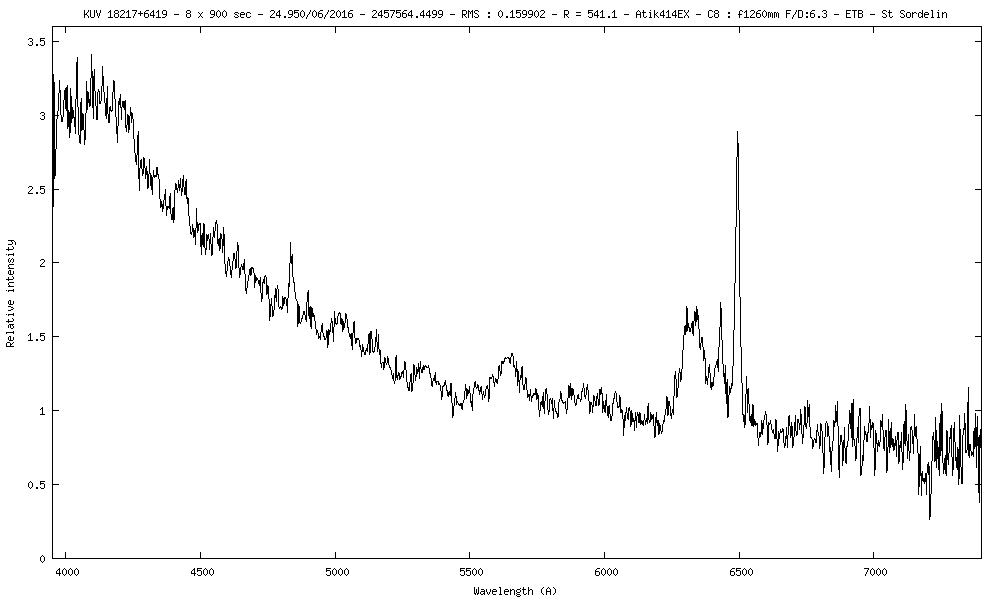
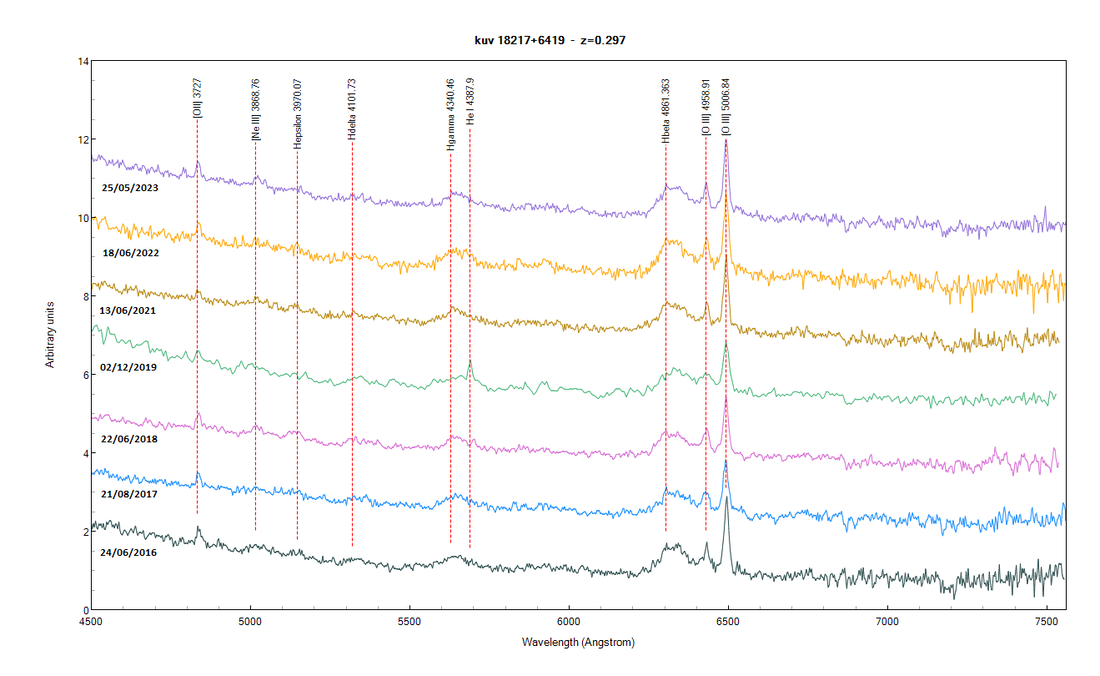
3) KUV 18217+6419 m=14.2 z=0.29718
| _kuv_18217-6419_20160624_908_etb.fit | |
| File Size: | 43 kb |
| File Type: | fit |
| _kuv18217_6419_20170821_972_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
| _kuv18217_64198_20180622_925_ebe.fit | |
| File Size: | 34 kb |
| File Type: | fit |
| _kuv18217_6419_20191202_766_ebe.fit | |
| File Size: | 14 kb |
| File Type: | fit |
| _kuv18217_6419_20210613_914_ebe.fit | |
| File Size: | 20 kb |
| File Type: | fit |
| _kuv18217_6419_20220618_015_ebe.fit | |
| File Size: | 28 kb |
| File Type: | fit |
| _kuv18217_6419_20230525_945_ebe.fit | |
| File Size: | 23 kb |
| File Type: | fit |
| _kuv18217_6419_20240604_939_ebe.fit | |
| File Size: | 23 kb |
| File Type: | fit |
Quasar KUV 18217+6419 :
[OIII] est mesurée à 6495A au repos à 4861.A.
z = (6495 - 5007) / 5007
z = 0.29718
d'ou une vitesse relativiste de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((0.29718+1)^2 - 1) / ((0.29718+1)^2 + 1)]
Vr = 299792.458 x (0.68267 / 2.68267)
Vr = 76 289.41 km/s
Distance :
D = Vr / Ho
D = 76 289.41 / 70
D = 1089.84 Mpc
[OIII] est mesurée à 6495A au repos à 4861.A.
z = (6495 - 5007) / 5007
z = 0.29718
d'ou une vitesse relativiste de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((0.29718+1)^2 - 1) / ((0.29718+1)^2 + 1)]
Vr = 299792.458 x (0.68267 / 2.68267)
Vr = 76 289.41 km/s
Distance :
D = Vr / Ho
D = 76 289.41 / 70
D = 1089.84 Mpc
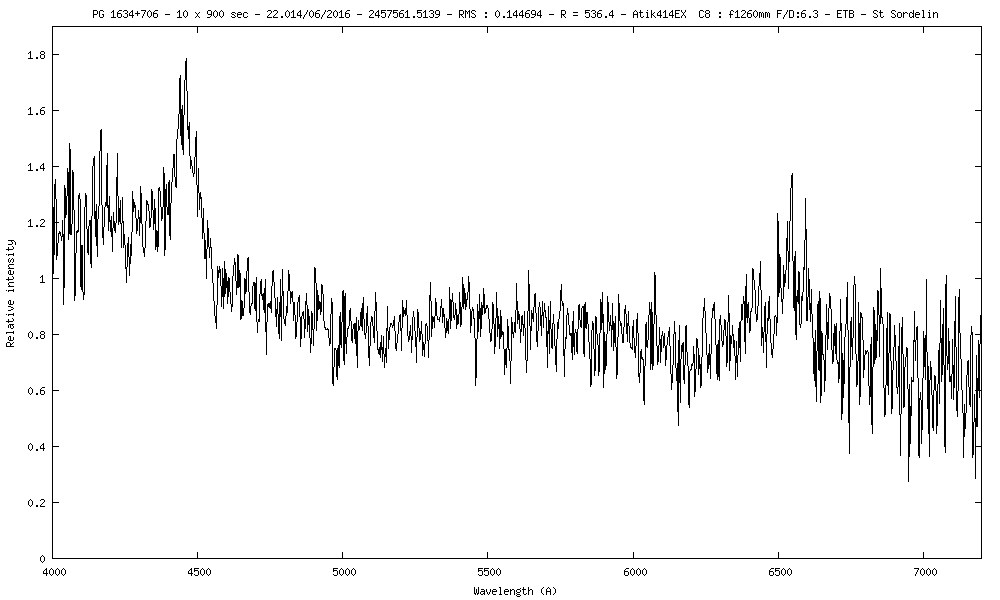
4) PG 1634+706 m=14.7 z=1.3365
| _pg1634-706_20160621_962_etb.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Nouvel essaie concluant sur le quasar PG 1634+706.
Belle nuit étoilée sans nuages, mais avec la pleine lune +1 jours. Donc l'instrumentation marche vraiment bien car le signal obtenue pour cette magnitude est plutôt bon. Ce quasar à une magnitude de 14.6
PG 1634 + 706 :
Le pic d'émission pour CIII] mesurée arrive pile à 4465.5A. Au repose il est à 1909A.
D'ou un redshift de :
z = ( 4460.5 - 1909 ) / 1909
z = 1.3365
Et une vitesse relativiste :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((1.3365+1)^2 - 1) / ((1.3365+1)^2 + 1)]
Vr = 299792.458 x (4.45923 / 6.45923)
Vr = 206 966.39 km/s
Simbad donne comme renseignements : z = 1.337 et Vr = 207 000 km/s
voici un site qui permet de calculer différents paramètres cosmologiques :
Belle nuit étoilée sans nuages, mais avec la pleine lune +1 jours. Donc l'instrumentation marche vraiment bien car le signal obtenue pour cette magnitude est plutôt bon. Ce quasar à une magnitude de 14.6
PG 1634 + 706 :
Le pic d'émission pour CIII] mesurée arrive pile à 4465.5A. Au repose il est à 1909A.
D'ou un redshift de :
z = ( 4460.5 - 1909 ) / 1909
z = 1.3365
Et une vitesse relativiste :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((1.3365+1)^2 - 1) / ((1.3365+1)^2 + 1)]
Vr = 299792.458 x (4.45923 / 6.45923)
Vr = 206 966.39 km/s
Simbad donne comme renseignements : z = 1.337 et Vr = 207 000 km/s
voici un site qui permet de calculer différents paramètres cosmologiques :
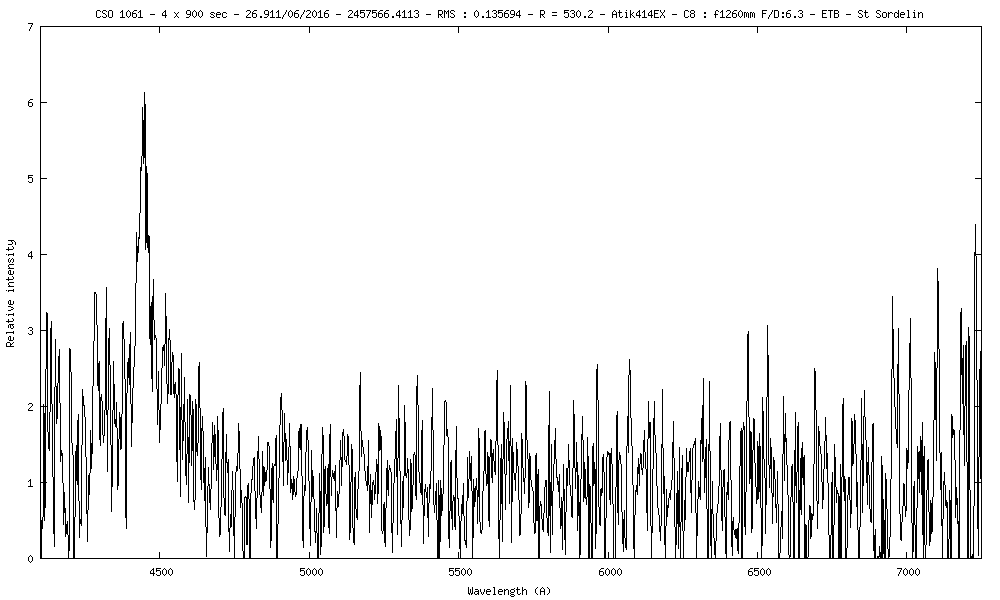
5) CSO1061 m=16.38 z=2.6621
| _cso1061_20160626_890_etb.fit | |
| File Size: | 43 kb |
| File Type: | fit |
La raie Lyman alpha est mesurée à 4449.5A; au repos elle est à 1215A.
z = (4449.5 - 1215) / 1215
z = 2.6621
d'ou une vitesse relativiste de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.6621+1)^2 - 1) / ((2.6621 +1)^2 + 1)]
Vr = 299792.458 x (12.41097 / 14.41097)
Vr = 258 186.31 km/s
D'ou une distance de regarde en arrière de 11.2 milliards d'années ! Les photons de ce quasar sont partis il y a 11.24 milliards d'années quand l'univers n'avait que 2.4 milliards d'années et une température de 6.38 K.
Pour comprendre sa distance, prenons la galaxie d'Andromède. Elle est a 2.53 millions d'années-lumières. Pour arriver à ce quasar il faudrait faire 4445 cette distance....
Plus curieux encore, du fais de l'expansion un photon émis au temps t1 par ce quasar sera reçu 11.24 milliards d'années plus tard, quand sa distance du fait de l'expansion sera de 20 milliards d'année-lumières (valeurs correspondant au temps de voyage de la lumière : source documetaire : Astronomie et astrophysiques d'Agnès Acker).
Pour un photon Lyman alpha a 1215Å observé a 4449.5Å, le facteur d'étirement est égal à (4449.5 / 1215) = 3.662139
Donc le facteur d’échelle au moment de l'émission était de :
a(t) = 1/3.662139
a(t) = 0.27306
Ce qui veut dire que depuis que les photons sont partis il y a 11.24 milliards d'années, l'univers a grandi de 72.7 %.
z = (4449.5 - 1215) / 1215
z = 2.6621
d'ou une vitesse relativiste de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.6621+1)^2 - 1) / ((2.6621 +1)^2 + 1)]
Vr = 299792.458 x (12.41097 / 14.41097)
Vr = 258 186.31 km/s
D'ou une distance de regarde en arrière de 11.2 milliards d'années ! Les photons de ce quasar sont partis il y a 11.24 milliards d'années quand l'univers n'avait que 2.4 milliards d'années et une température de 6.38 K.
Pour comprendre sa distance, prenons la galaxie d'Andromède. Elle est a 2.53 millions d'années-lumières. Pour arriver à ce quasar il faudrait faire 4445 cette distance....
Plus curieux encore, du fais de l'expansion un photon émis au temps t1 par ce quasar sera reçu 11.24 milliards d'années plus tard, quand sa distance du fait de l'expansion sera de 20 milliards d'année-lumières (valeurs correspondant au temps de voyage de la lumière : source documetaire : Astronomie et astrophysiques d'Agnès Acker).
Pour un photon Lyman alpha a 1215Å observé a 4449.5Å, le facteur d'étirement est égal à (4449.5 / 1215) = 3.662139
Donc le facteur d’échelle au moment de l'émission était de :
a(t) = 1/3.662139
a(t) = 0.27306
Ce qui veut dire que depuis que les photons sont partis il y a 11.24 milliards d'années, l'univers a grandi de 72.7 %.
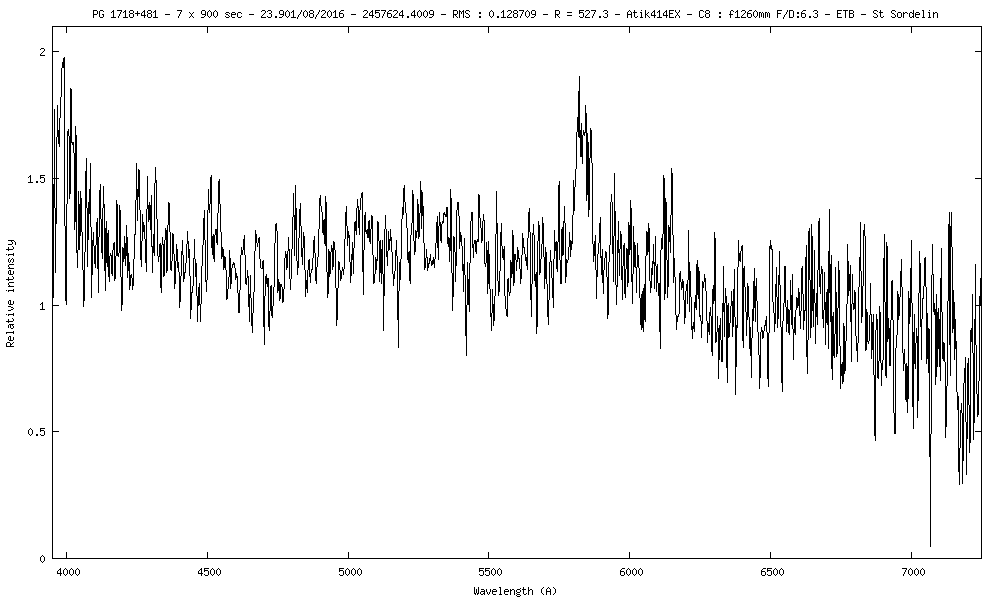
6) PG1718+481 m=14.6 z=1.08
| _pg1717_481_20160823_863_etb.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Le pic de la raie du MgII est mesurée à 5821A ; au repos elle est à 2798A.
z = (5821 - 2798) / 2798
z = 1.08
d'ou une vitesse relativiste de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((1.08+1)^2 - 1) / ((1.08 +1)^2 + 1)]
Vr = 299792.458 x (3.3264 / 5.3264)
Vr = 187 223.94 km/s
On trouve une distance de regard en arrière de 8.128 milliards d'années. Avec l'expansion de l'univers cette distance est maintenant réellement de 11.56 millards d'années lumières.
Le facteur d’échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 1.08)
a(t) = 0.4807
Depuis le départ des photons l'Univers s'est agrandi de 51.92 % et la température de l'Univers était de 4.805 K.
z = (5821 - 2798) / 2798
z = 1.08
d'ou une vitesse relativiste de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((1.08+1)^2 - 1) / ((1.08 +1)^2 + 1)]
Vr = 299792.458 x (3.3264 / 5.3264)
Vr = 187 223.94 km/s
On trouve une distance de regard en arrière de 8.128 milliards d'années. Avec l'expansion de l'univers cette distance est maintenant réellement de 11.56 millards d'années lumières.
Le facteur d’échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 1.08)
a(t) = 0.4807
Depuis le départ des photons l'Univers s'est agrandi de 51.92 % et la température de l'Univers était de 4.805 K.
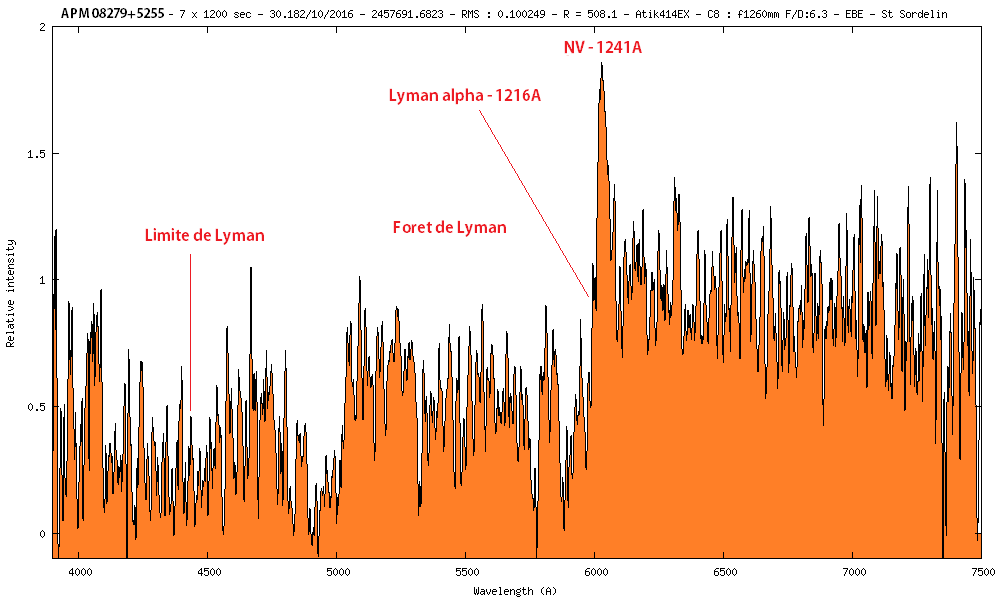
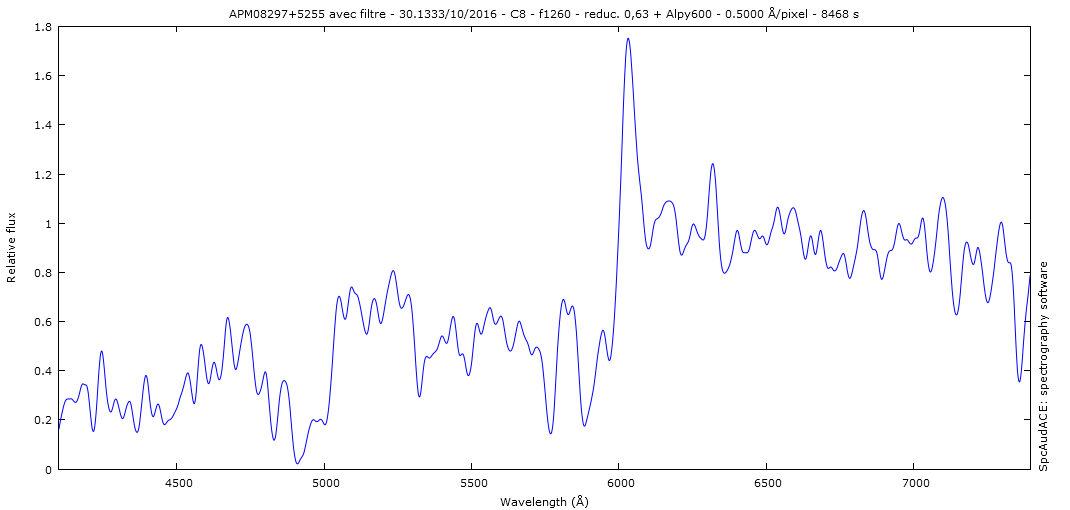
7) APM 08279+5255 m=15.2 z=3.8573
| _apm08279_5255_20161030_133_ebe.fit | |
| File Size: | 40 kb |
| File Type: | fit |
Avec la raie NV à 1241A qui arrive à 6028A sur le spectre, on trouve un redshift de 3.8573 assez proche du 3.91 de Simbad (télescope de 20 cm de diamètre):
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (6028 - 1241) / 1241
z = 3.8573
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.8573+1)^2 - 1) / ((3.8573 +1)^2 + 1)]
Vr = 299792.458 x (22.59 / 24.59)
Vr = 275 409 km/s [+/- 50km/s]
La distance de regard en arrière de 12.095 milliards d'années. Les photons sont partis quand l'Univers avait 1.625 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.8573)
a(t) = 0.2058
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~80 % !
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.8573)) / (1+0)
T(t1) = 13.236 K
La température de l'Univers était de 13.236 K (plus ~5 (4.857) fois la température actuelle).
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (6028 - 1241) / 1241
z = 3.8573
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.8573+1)^2 - 1) / ((3.8573 +1)^2 + 1)]
Vr = 299792.458 x (22.59 / 24.59)
Vr = 275 409 km/s [+/- 50km/s]
La distance de regard en arrière de 12.095 milliards d'années. Les photons sont partis quand l'Univers avait 1.625 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.8573)
a(t) = 0.2058
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~80 % !
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.8573)) / (1+0)
T(t1) = 13.236 K
La température de l'Univers était de 13.236 K (plus ~5 (4.857) fois la température actuelle).
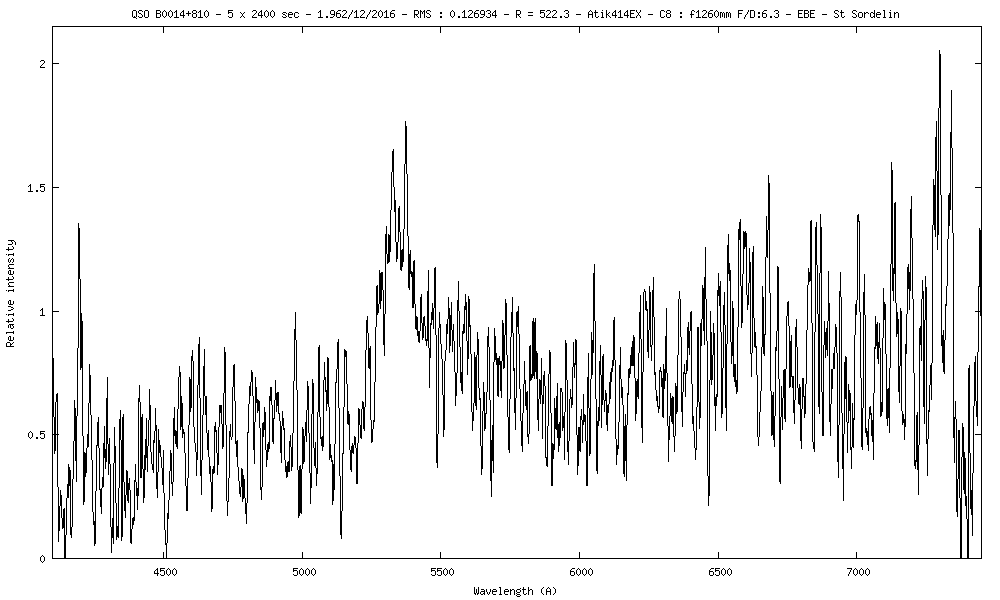
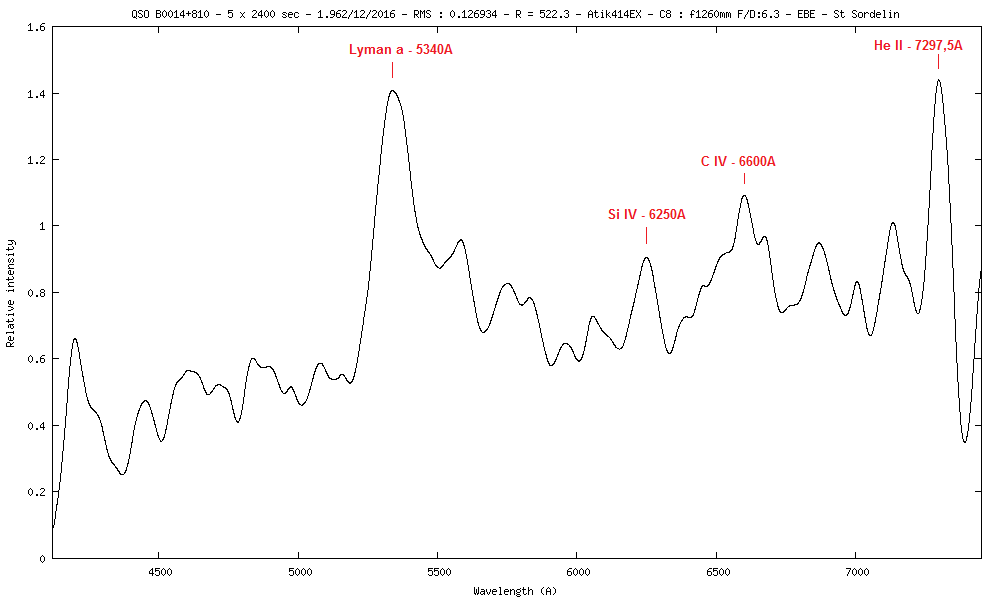
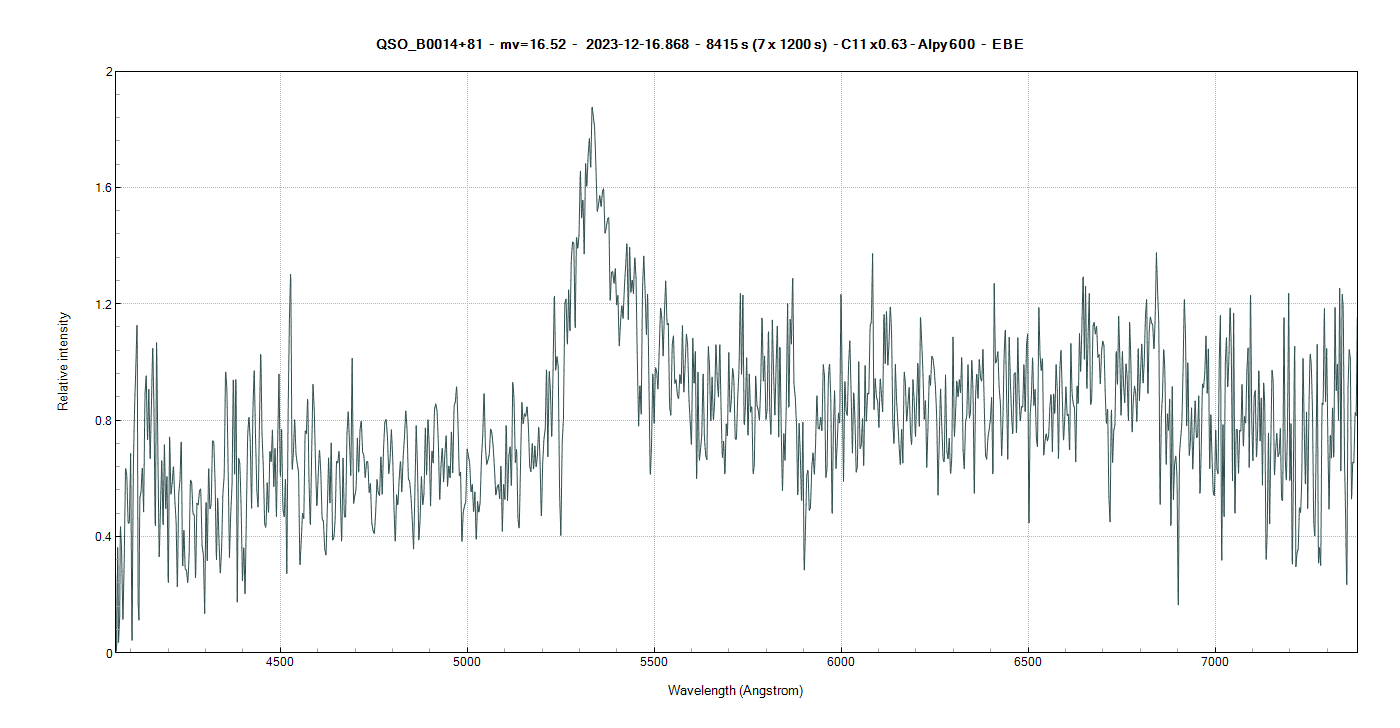
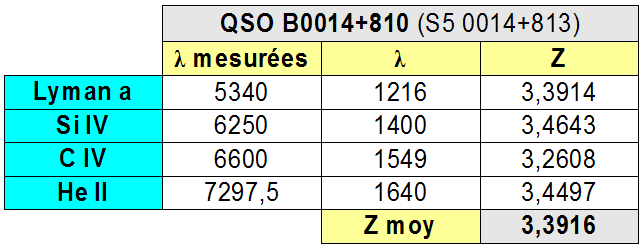
8) QSO B0014+810 ou S5 0014+813 m=16.52 z=3.3916 (Simbad : Z=3.366)
Wikipédia :
S5 0014+810 (m=16.5) est un quasar ou blazar FSRQ lointain situé dans la constellation de Céphée. Il fait partie d'une galaxie elliptique géante à sursauts de formation d'étoiles.
S5 0014+81 est l'un des quasars les plus lumineux connus et possède l'un des trous noirs les plus massifs jamais recensés, d'une masse estimée à 40 milliards de masses solaires (M☉).
Caractéristiques :
S5 0014+81 est l'un des blazars les plus lumineux connus, dégageant une énergie dépassant les 10^41 watts. Sa magnitude bolométrique absolue est de -31,5 pour une luminosité de 3 846×10^14 fois celle du Soleil, soit l'équivalent de 25000 Voie Lactée !!
Comme les autres blazars, S5 0014+81 possède un trou noir supermassif en son centre qui pourrait être à l'origine de son intense activité.
En 2009, une équipe d'astronome utilisant le télescope spatial SWIFT a déterminé la masse de ce dernier à l'aide de la luminosité bolométrique. Ils ont obtenu une valeur 10 000 fois plus élevée que celle du trou noir situé au centre de la Voie lactée, soit environ 40 milliards de M☉. Cela en fait le trou noir le plus massif connu, plus de six fois plus massif que celui situé au centre de la galaxie elliptique M87, qui a détenu le record pendant 60 ans.
Un tel astre présenterait un rayon de Schwarzschild de 120 milliards de km. L'horizon externe du trou noir présente donc un diamètre de 240 milliards de km,soit environ 1 600 unités astronomiques. Ce diamètre correspond à celui de l'ergosphère. Ce trou noir transformerait l'équivalent de 4 000 M☉ chaque année.
Apparu seulement 1,6 milliards d'années après le Big Bang, il laisse croire que les trous noirs supermassifs sont apparus très rapidement dans l'histoire de l'Univers.
S5 0014+810 (m=16.5) est un quasar ou blazar FSRQ lointain situé dans la constellation de Céphée. Il fait partie d'une galaxie elliptique géante à sursauts de formation d'étoiles.
S5 0014+81 est l'un des quasars les plus lumineux connus et possède l'un des trous noirs les plus massifs jamais recensés, d'une masse estimée à 40 milliards de masses solaires (M☉).
Caractéristiques :
S5 0014+81 est l'un des blazars les plus lumineux connus, dégageant une énergie dépassant les 10^41 watts. Sa magnitude bolométrique absolue est de -31,5 pour une luminosité de 3 846×10^14 fois celle du Soleil, soit l'équivalent de 25000 Voie Lactée !!
Comme les autres blazars, S5 0014+81 possède un trou noir supermassif en son centre qui pourrait être à l'origine de son intense activité.
En 2009, une équipe d'astronome utilisant le télescope spatial SWIFT a déterminé la masse de ce dernier à l'aide de la luminosité bolométrique. Ils ont obtenu une valeur 10 000 fois plus élevée que celle du trou noir situé au centre de la Voie lactée, soit environ 40 milliards de M☉. Cela en fait le trou noir le plus massif connu, plus de six fois plus massif que celui situé au centre de la galaxie elliptique M87, qui a détenu le record pendant 60 ans.
Un tel astre présenterait un rayon de Schwarzschild de 120 milliards de km. L'horizon externe du trou noir présente donc un diamètre de 240 milliards de km,soit environ 1 600 unités astronomiques. Ce diamètre correspond à celui de l'ergosphère. Ce trou noir transformerait l'équivalent de 4 000 M☉ chaque année.
Apparu seulement 1,6 milliards d'années après le Big Bang, il laisse croire que les trous noirs supermassifs sont apparus très rapidement dans l'histoire de l'Univers.
Spectre obtenu assez bruité mais avec de longues (2400s) :
| _qso_b0014_810_20161201_887_ebe.fit | |
| File Size: | 40 kb |
| File Type: | fit |
| _qso_b0014_81_20231216_868_ebe.fit | |
| File Size: | 20 kb |
| File Type: | fit |
| _qso_b0014_810_20161201_887_ebe_filtre.fit | |
| File Size: | 31 kb |
| File Type: | fit |
Assez proche des résultats de Simbad qui donne z=3.366
Puis quelques mesures :
QSO B0014+810 a une vitesse relativiste de recession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.3916+1)^2 - 1) / ((3.3916 +1)^2 + 1)]
Vr = 299792.458 x (18.286 / 20.286)
Vr = 270 235,9 km/s [+/- 50km/s]
Puis quelques mesures :
QSO B0014+810 a une vitesse relativiste de recession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.3916+1)^2 - 1) / ((3.3916 +1)^2 + 1)]
Vr = 299792.458 x (18.286 / 20.286)
Vr = 270 235,9 km/s [+/- 50km/s]
La distance de regard en arrière de 11.83 milliards d'années. Les photons sont partis quand l'Univers avait 1.87 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 22.317 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.3916)
a(t) = 0.2277
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~77.3 % ! Maintenant le rayon est plus grand de 1/a(t) = 339 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = (2,725 x (1 + 3.3916) / (1+0)
T(t1) = 11.96 K
La température de l'Univers était de 11.96 K (plus ~4.4 fois la température actuelle).
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.3916)
a(t) = 0.2277
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~77.3 % ! Maintenant le rayon est plus grand de 1/a(t) = 339 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = (2,725 x (1 + 3.3916) / (1+0)
T(t1) = 11.96 K
La température de l'Univers était de 11.96 K (plus ~4.4 fois la température actuelle).
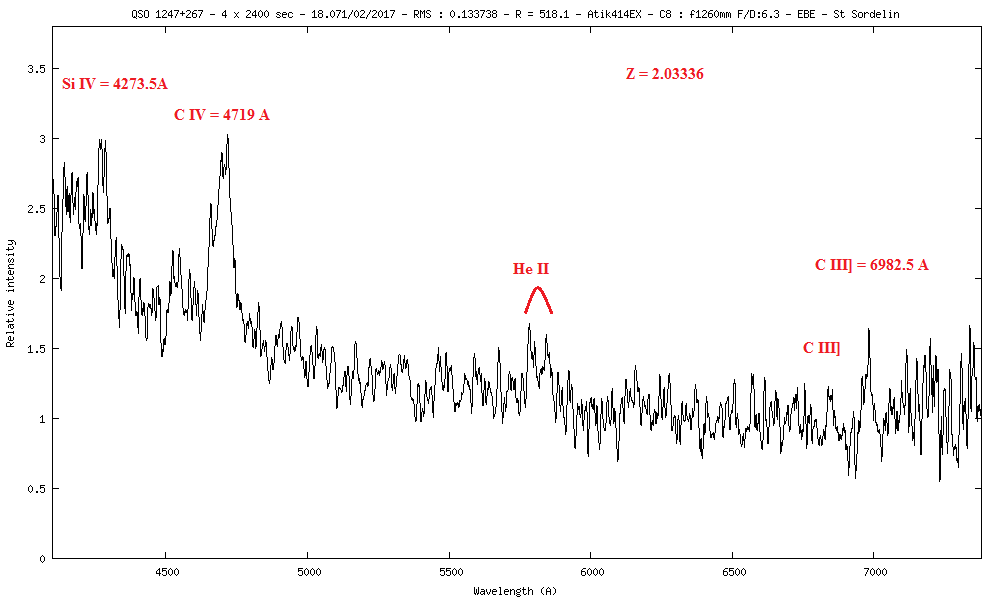
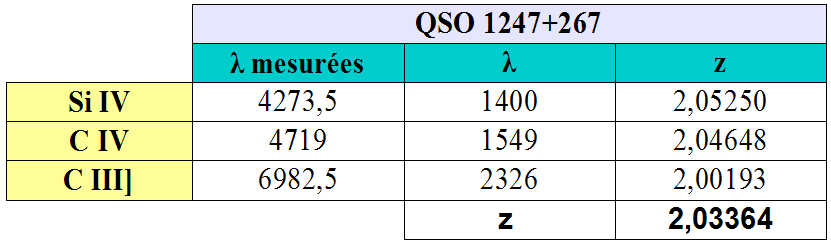
9) QSO 1247+267 m=15.92 z=2.03364 (Simbad : Z=2.04758)
| _qso1247_267_20170218_015_ebe.fit | |
| File Size: | 31 kb |
| File Type: | fit |
QSO 1247+267 a une vitesse relativiste de récession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.03364+1)^2 - 1) / ((2.03364 +1)^2 + 1)]
Vr = 299792.458 x (8.20297 / 10.20297)
Vr = 241 026.73 km/s [+/- 50km/s]
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.03364+1)^2 - 1) / ((2.03364 +1)^2 + 1)]
Vr = 299792.458 x (8.20297 / 10.20297)
Vr = 241 026.73 km/s [+/- 50km/s]
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 17.36milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.03364)
a(t) = 0.329637
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~67 % ! Maintenant le rayon est plus grand de 1/a(t) = 203.3 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = (2,725 x (1 + 2.03364) / (1+0)
T(t1) = 8.266 K
La température de l'Univers était de 8.266 K (plus ~3 fois la température actuelle).
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.03364)
a(t) = 0.329637
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~67 % ! Maintenant le rayon est plus grand de 1/a(t) = 203.3 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = (2,725 x (1 + 2.03364) / (1+0)
T(t1) = 8.266 K
La température de l'Univers était de 8.266 K (plus ~3 fois la température actuelle).
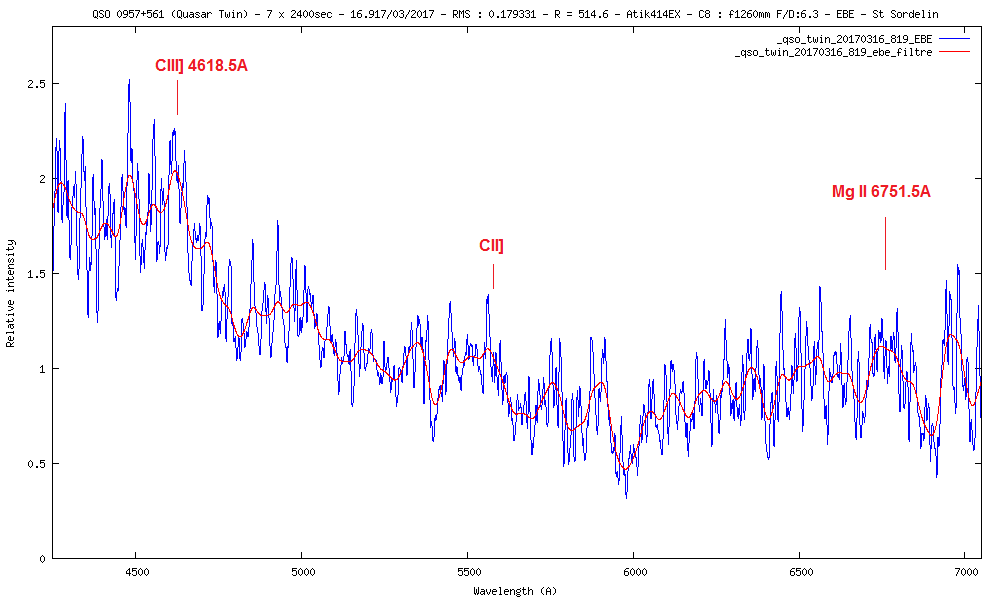
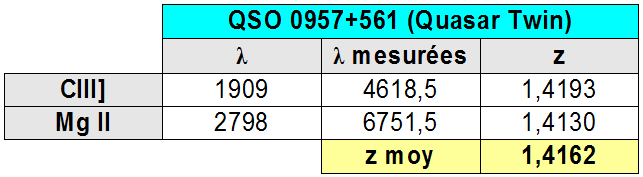
10) Quasar Twin QSO0957+561 m=16.7 z=1.4162
| _qso_twin_20170316_819_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
| _qso_twin_20170316_819_ebe_filtre.fit | |
| File Size: | 25 kb |
| File Type: | fit |
QSO 1247+267 a une vitesse relativiste de récession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 212 108.2 km/s [+/- 50km/s]
Le temps de regard en arrière est de 9.2 millards d'années (voyage de la lumière pour nous parvenir) et l'Univers était agé de 4.5 millards d'années. Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 13.94 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.7325)
a(t) = 0.4138
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~58.6 % ! Maintenant le rayon est plus grand de 1/a(t) = 141.6 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t1) = 3.85K
La température de l'Univers était de 3.85K (plus ~1.41 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur des raies en émission à mi-hauteur (FWHM).
CIII] a une largeur de 56A et MgII à une largeur de 90A
Avec la formule V = (Delta lambda / lambda) x c
On trouve des vitesses de 8794km/s et 9643kms, d'ou une moyenne de 9218.5km/s
La vitesse de rotation du disque d'accrétion dans ce Quasar est de 9218.5 km/s.
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 212 108.2 km/s [+/- 50km/s]
Le temps de regard en arrière est de 9.2 millards d'années (voyage de la lumière pour nous parvenir) et l'Univers était agé de 4.5 millards d'années. Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 13.94 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.7325)
a(t) = 0.4138
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~58.6 % ! Maintenant le rayon est plus grand de 1/a(t) = 141.6 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t1) = 3.85K
La température de l'Univers était de 3.85K (plus ~1.41 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur des raies en émission à mi-hauteur (FWHM).
CIII] a une largeur de 56A et MgII à une largeur de 90A
Avec la formule V = (Delta lambda / lambda) x c
On trouve des vitesses de 8794km/s et 9643kms, d'ou une moyenne de 9218.5km/s
La vitesse de rotation du disque d'accrétion dans ce Quasar est de 9218.5 km/s.
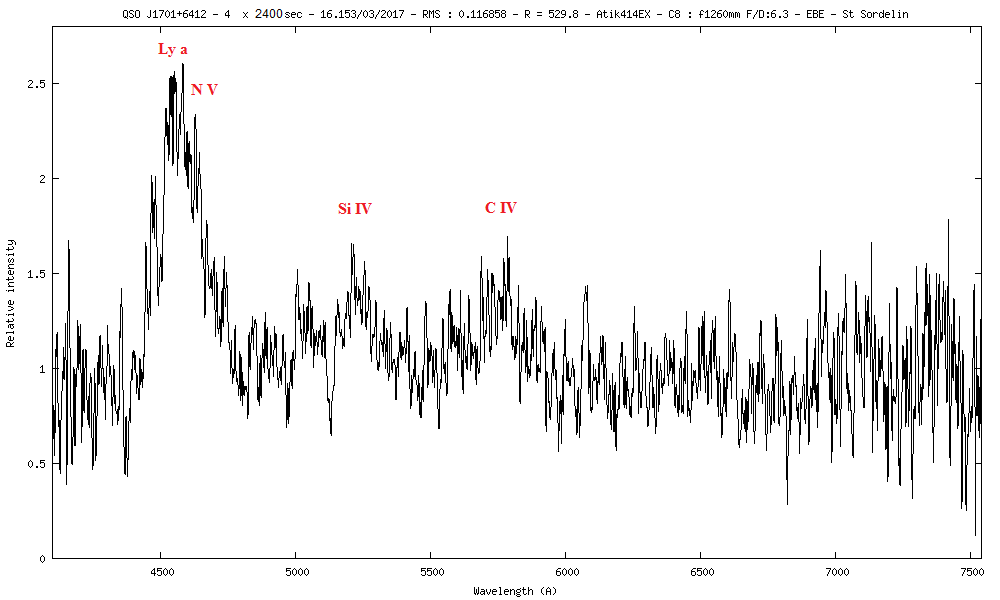
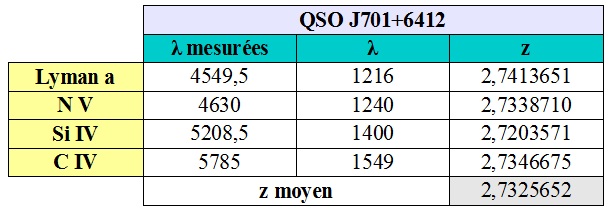
11) QSO j1701+6412 m=16.17 z=2.7325
| _qso_j1701_6412_20170316_097_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
QSO 1247+267 a une vitesse relativiste de récession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 259 636.75 km/s [+/- 50km/s]
Le temps de regard en arrière est de 11.31 milliards d'années (voyage de la lumière pour nous parvenir) et l'Univers était âgé de 2.4 milliards d'années. Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 20.23 milliards d'années lumières.
Le facteur d'échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.7325)
a(t) = 0.268
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~73.2 % ! Maintenant le rayon est plus grand de 1/a(t) = 273.13 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t1) = 10.17K
La température de l'Univers était de 10.17 K (plus ~3.73 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 142A
V = (Delta lambda / lambda) x c
V = (54 / 1216) x 299792.458
V = 13 313 km/s
De même Si IV et C IV ont des largeurs de ~95A et ~87A ce qui fait des vitesses de 20 343 km/s et 16 838 km/s.
En moyennant ces largeurs des raies, on trouve une vitesse de rotation du disque d'accrétion de 16 831 km/s.
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 259 636.75 km/s [+/- 50km/s]
Le temps de regard en arrière est de 11.31 milliards d'années (voyage de la lumière pour nous parvenir) et l'Univers était âgé de 2.4 milliards d'années. Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 20.23 milliards d'années lumières.
Le facteur d'échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.7325)
a(t) = 0.268
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~73.2 % ! Maintenant le rayon est plus grand de 1/a(t) = 273.13 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t1) = 10.17K
La température de l'Univers était de 10.17 K (plus ~3.73 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 142A
V = (Delta lambda / lambda) x c
V = (54 / 1216) x 299792.458
V = 13 313 km/s
De même Si IV et C IV ont des largeurs de ~95A et ~87A ce qui fait des vitesses de 20 343 km/s et 16 838 km/s.
En moyennant ces largeurs des raies, on trouve une vitesse de rotation du disque d'accrétion de 16 831 km/s.
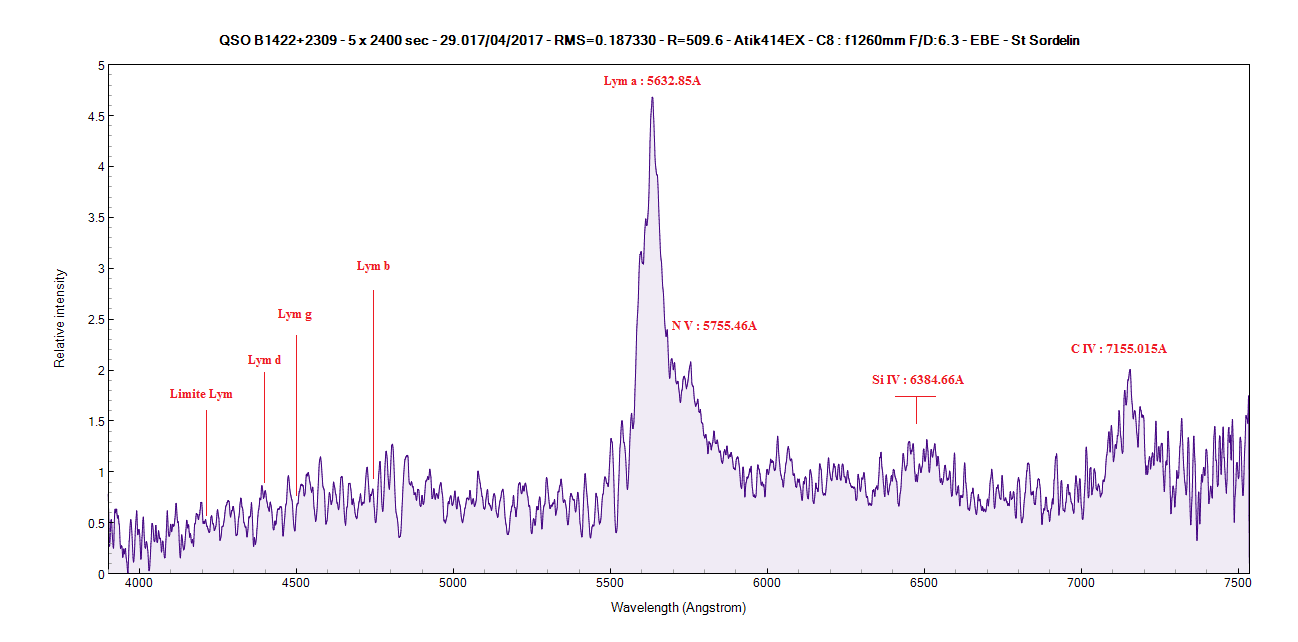
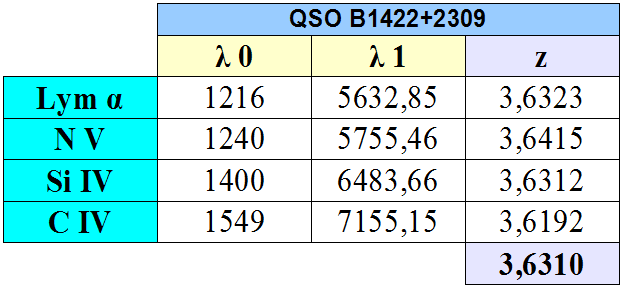
12) QSO B1422+2309 m=15.84 z=3.631
| _qso-b1422_2309_20170428_947_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
QSO B1422+2309 a une vitesse relativiste de récession de :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 273 080 km/s [+/- 50km/s]
Le temps de regard en arrière est de 11.97 milliards d'années (voyage de la lumière pour nous parvenir) et l'Univers était âgé de 1.74 milliards d'années. Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 22.96 milliards d'années lumières.
Le facteur d'échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.631)
a(t) = 0.2159
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~78.4 % ! Maintenant le rayon est plus grand de 1/a(t) = 363.17 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t1) = 12.62K
La température de l'Univers était de 12.61 K (plus ~4.631 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 142A
V = (Delta lambda / lambda) x c
V = (122 / 1216) x 299792.458
V = 30 077.9 km/s
De même Si IVa une largeur de ~142.5A ce qui fait une vitesse de 27 579 km/s.
En moyennant ces largeurs des raies, on trouve une vitesse de rotation du disque d'accrétion de 28 828.45 km/s.
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 273 080 km/s [+/- 50km/s]
Le temps de regard en arrière est de 11.97 milliards d'années (voyage de la lumière pour nous parvenir) et l'Univers était âgé de 1.74 milliards d'années. Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 22.96 milliards d'années lumières.
Le facteur d'échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.631)
a(t) = 0.2159
Ce qui veut dire qu'à l'époque ou les photons sont partis l'Univers était plus petit de ~78.4 % ! Maintenant le rayon est plus grand de 1/a(t) = 363.17 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grâce au redshift ;
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t1) = 12.62K
La température de l'Univers était de 12.61 K (plus ~4.631 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 142A
V = (Delta lambda / lambda) x c
V = (122 / 1216) x 299792.458
V = 30 077.9 km/s
De même Si IVa une largeur de ~142.5A ce qui fait une vitesse de 27 579 km/s.
En moyennant ces largeurs des raies, on trouve une vitesse de rotation du disque d'accrétion de 28 828.45 km/s.
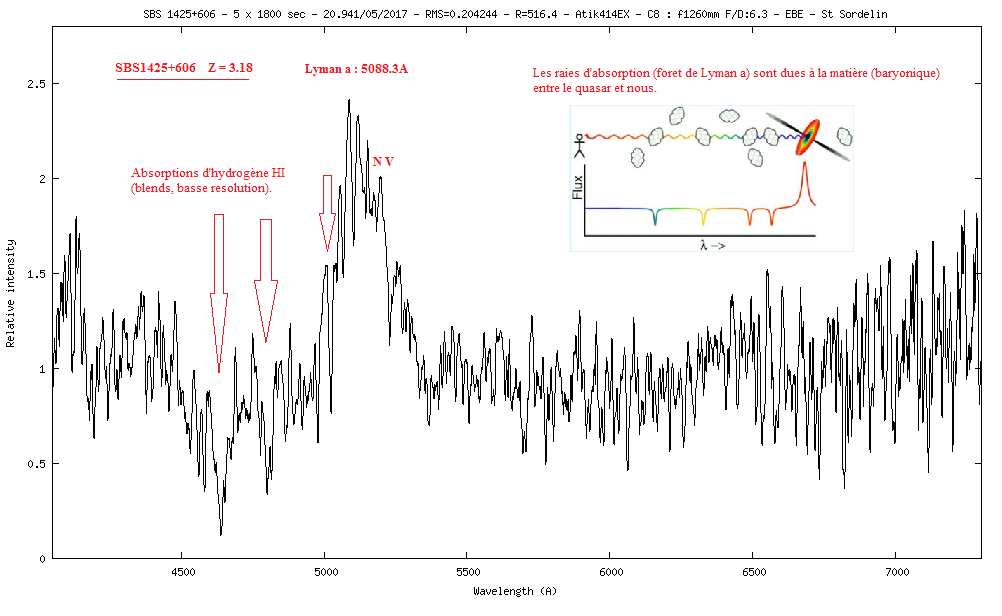
13) SBS 1425+606 m=16.5 z=3.18446
| _sbs1425_606_20170520_889_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Avec la raie Lyman-a à 1216A qui arrive à 5088.3A sur le spectre, on trouve un redshift de 3.18446
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (5088.3- 1216) / 1216
z = 3.18446
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.18446+1)^2 - 1) / ((3.18446+1)^2 + 1)]
Vr = 299792.458 x (16.51/ 18.51)
Vr = 267 400 km/s [+/- 50km/s]
La distance de regard en arrière de 11.69 milliards d'années. Les photons sont partis quand l'Univers avait 2.03 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.18446)
a(t) = 0.239
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~76 % ! Maintenant le rayon est plus grand de 1/a(t) = 318.4 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.18446)) / (1+0)
T(t1) = 11.4 K
La température de l'Univers était de 11.4 K (plus ~4 (4.18) fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 138.5A
V = (Delta lambda / lambda) x c
V = (138.5 / 1216) x 299792.458
V = 34 145 km/s
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (5088.3- 1216) / 1216
z = 3.18446
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.18446+1)^2 - 1) / ((3.18446+1)^2 + 1)]
Vr = 299792.458 x (16.51/ 18.51)
Vr = 267 400 km/s [+/- 50km/s]
La distance de regard en arrière de 11.69 milliards d'années. Les photons sont partis quand l'Univers avait 2.03 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.18446)
a(t) = 0.239
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~76 % ! Maintenant le rayon est plus grand de 1/a(t) = 318.4 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.18446)) / (1+0)
T(t1) = 11.4 K
La température de l'Univers était de 11.4 K (plus ~4 (4.18) fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 138.5A
V = (Delta lambda / lambda) x c
V = (138.5 / 1216) x 299792.458
V = 34 145 km/s
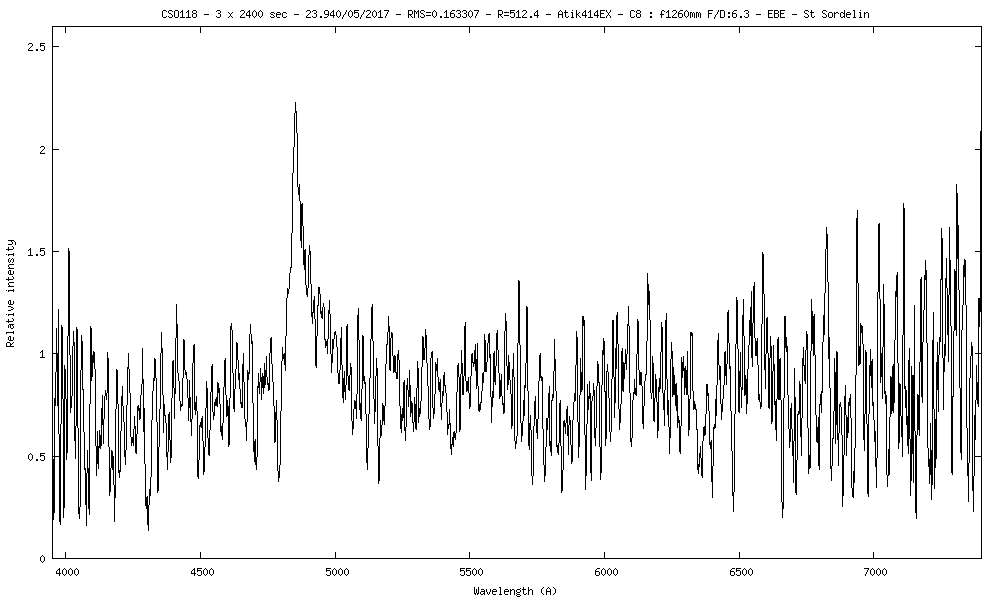
14) CSO118 m=16.47 z=2.99
| _cso118_20170523_898_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Avec la raie Lyman-a à 1216A qui arrive à 4852.5A sur le spectre, on trouve un redshift de 2.99
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4852.5- 1216) / 1216
z = 2.99
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.99+1)^2 - 1) / ((299+1)^2 + 1)]
Vr = 299792.458 x (14.92/ 16.92)
Vr = 264 355 km/s [+/- 50km/s]
La distance de regard en arrière de 11.54 milliards d'années. Les photons sont partis quand l'Univers avait 2.18 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.99)
a(t) = 0.2506
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~75 % ! Maintenant le rayon est plus grand de 1/a(t) = 299 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.18446)) / (1+0)
T(t1) = 10.87 K
La température de l'Univers était de 10.87 K (plus ~4 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 80A
V = (Delta lambda / lambda) x c
V = (80 / 1216) x 299792.458
V = 19 723 km/s
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4852.5- 1216) / 1216
z = 2.99
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.99+1)^2 - 1) / ((299+1)^2 + 1)]
Vr = 299792.458 x (14.92/ 16.92)
Vr = 264 355 km/s [+/- 50km/s]
La distance de regard en arrière de 11.54 milliards d'années. Les photons sont partis quand l'Univers avait 2.18 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.99)
a(t) = 0.2506
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~75 % ! Maintenant le rayon est plus grand de 1/a(t) = 299 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.18446)) / (1+0)
T(t1) = 10.87 K
La température de l'Univers était de 10.87 K (plus ~4 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 80A
V = (Delta lambda / lambda) x c
V = (80 / 1216) x 299792.458
V = 19 723 km/s
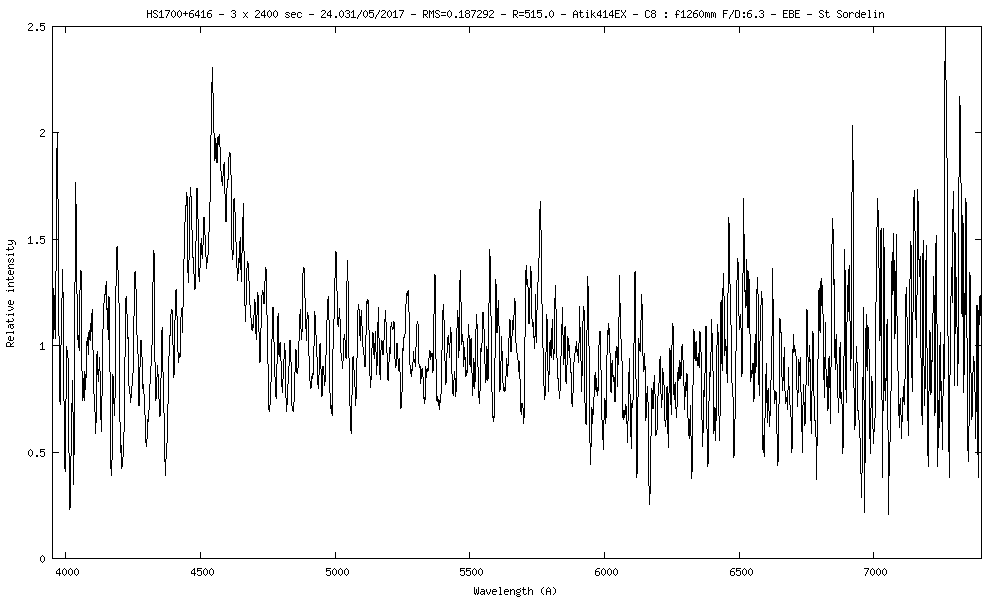
15) HS1700+6416 m=16.17 z=2.737
| _hs1700_6416_20170523_990_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Avec la raie Lyman-a à 1216A qui arrive à 4544A sur le spectre, on trouve un redshift de 2.737
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4544- 1216) / 1216
z = 2.737
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.737+1)^2 - 1) / ((2.737+1)^2 + 1)]
Vr = 299792.458 x (12.965/ 14.965)
Vr = 259 726 km/s [+/- 50km/s]
La distance de regard en arrière de 11.32 milliards d'années. Les photons sont partis quand l'Univers avait 2.4 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.737)
a(t) = 0.2676
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~73.2 % ! Maintenant le rayon est plus grand de 1/a(t) = 273.7 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 2.737)) / (1+0)
T(t1) = 10.18 K
La température de l'Univers était de 10.18 K (plus ~3.73 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 120A
V = (Delta lambda / lambda) x c
V = (120 / 1216) x 299792.458
V = 29 584 km/s
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4544- 1216) / 1216
z = 2.737
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.737+1)^2 - 1) / ((2.737+1)^2 + 1)]
Vr = 299792.458 x (12.965/ 14.965)
Vr = 259 726 km/s [+/- 50km/s]
La distance de regard en arrière de 11.32 milliards d'années. Les photons sont partis quand l'Univers avait 2.4 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.737)
a(t) = 0.2676
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~73.2 % ! Maintenant le rayon est plus grand de 1/a(t) = 273.7 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 2.737)) / (1+0)
T(t1) = 10.18 K
La température de l'Univers était de 10.18 K (plus ~3.73 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 120A
V = (Delta lambda / lambda) x c
V = (120 / 1216) x 299792.458
V = 29 584 km/s
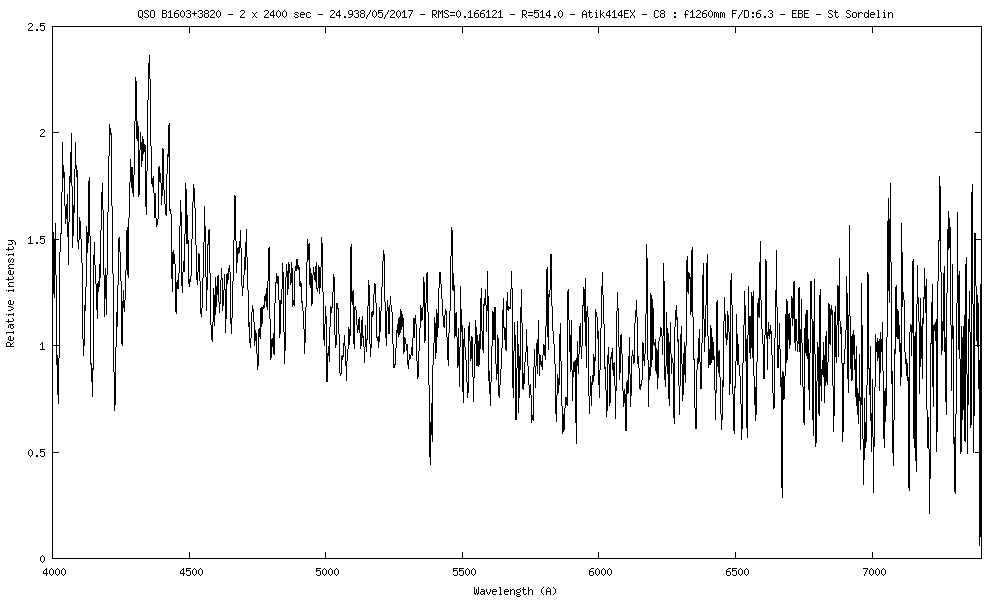
16) QSO B1603+3820 m=15.99 z=2.58
| _qsob1603_3820_20170524_910_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Avec la raie Lyman-a à 1216A qui arrive à 4355A sur le spectre, on trouve un redshift de 2.58
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4355- 1216) / 1216
z = 2.58
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.58+1)^2 - 1) / ((2.58+1)^2 + 1)]
Vr = 299792.458 x (11.81/ 13.81)
Vr = 256 375 km/s [+/- 50km/s]
La distance de regard en arrière de 11.16 milliards d'années. Les photons sont partis quand l'Univers avait 2.56 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.58)
a(t) = 0.2793
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~72 % ! Maintenant le rayon est plus grand de 1/a(t) = 258 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 2.58)) / (1+0)
T(t1) = 11.4 K
La température de l'Univers était de 9.75 K (plus ~3.58) fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 116A
V = (Delta lambda / lambda) x c
V = (116 / 1216) x 299792.458
V = 28 598 km/s
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4355- 1216) / 1216
z = 2.58
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.58+1)^2 - 1) / ((2.58+1)^2 + 1)]
Vr = 299792.458 x (11.81/ 13.81)
Vr = 256 375 km/s [+/- 50km/s]
La distance de regard en arrière de 11.16 milliards d'années. Les photons sont partis quand l'Univers avait 2.56 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.58)
a(t) = 0.2793
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~72 % ! Maintenant le rayon est plus grand de 1/a(t) = 258 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 2.58)) / (1+0)
T(t1) = 11.4 K
La température de l'Univers était de 9.75 K (plus ~3.58) fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 116A
V = (Delta lambda / lambda) x c
V = (116 / 1216) x 299792.458
V = 28 598 km/s
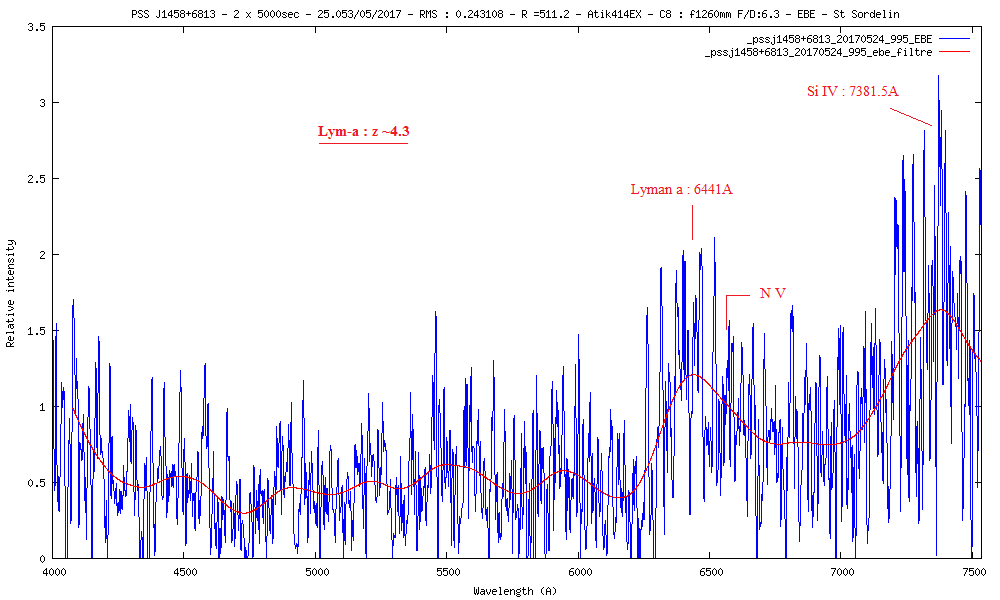
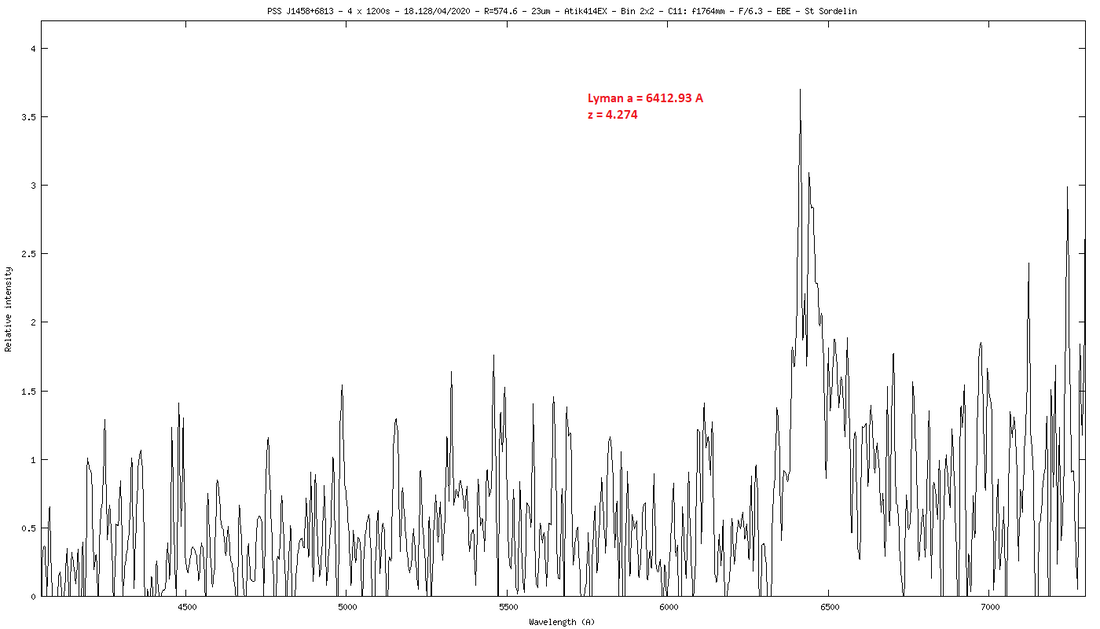
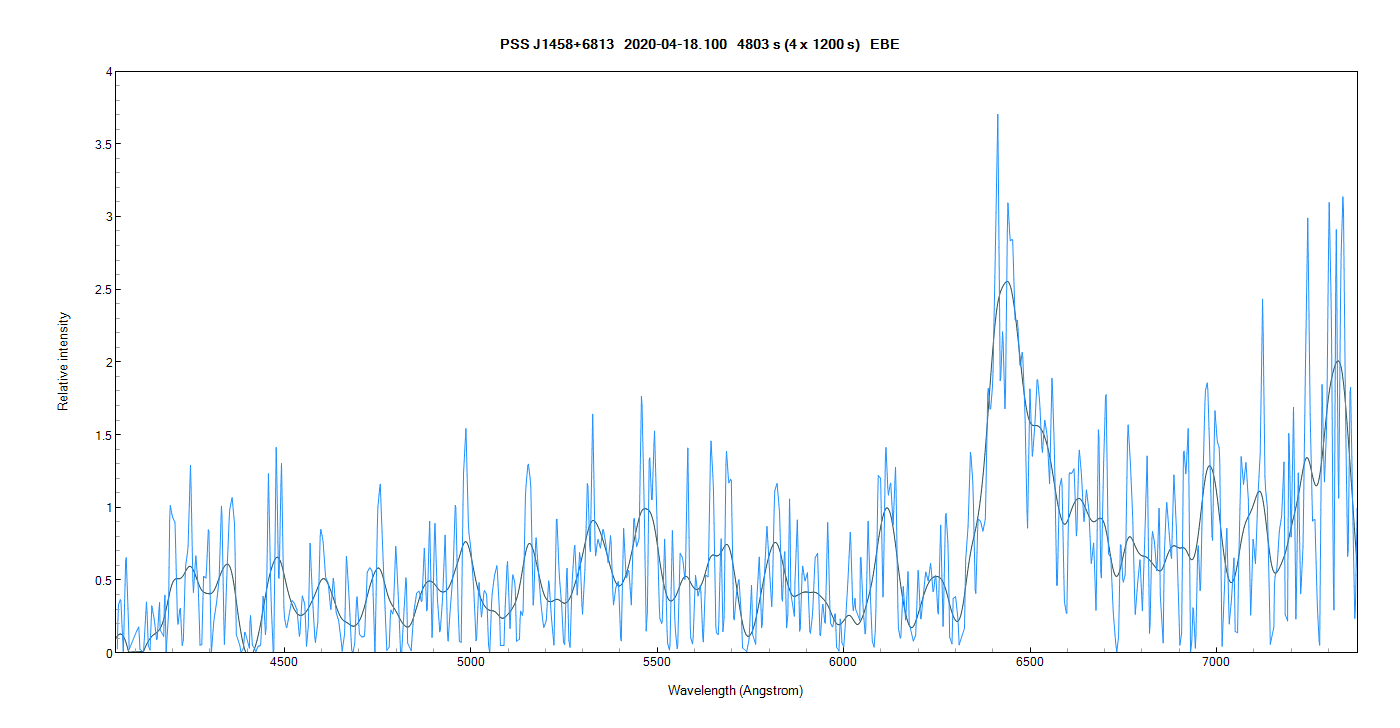
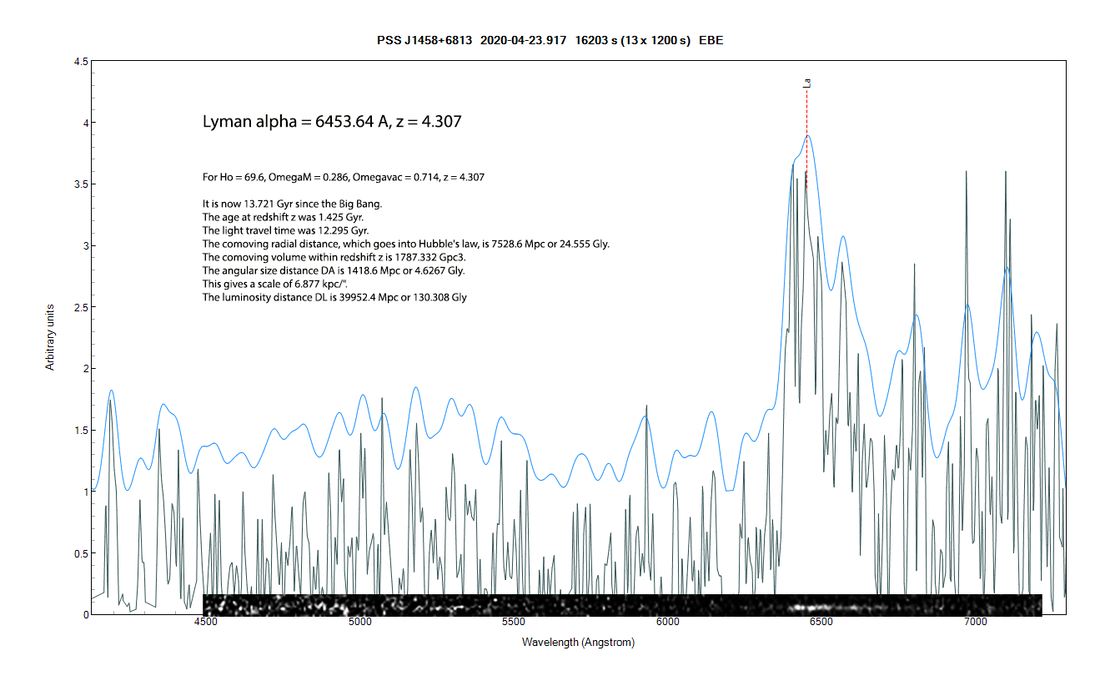
17) PSS J1458+6813 m=18.37 z=4.3
| _pssj1458_6813_20170524_995_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
| _pssj1458_6813_20170524_995_ebe_filtre.fit | |
| File Size: | 31 kb |
| File Type: | fit |
| _pssj1458_6813_20200418_100_ebe.fit | |
| File Size: | 11 kb |
| File Type: | fit |
Avec la raie Lyman-a à 1216A qui arrive à 6453A sur le spectre, on trouve un redshift de 4.3
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (6453- 1216) / 1216
z = 4.3
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((4.3+1)^2 - 1) / ((4.3+1)^2 + 1)]
Vr = 299792.458 x (27.09/ 29.09)
Vr = 279 181 km/s [+/- 50km/s]
La distance de regard en arrière de 12.29 milliards d'années. Les photons sont partis quand l'Univers avait 1.43 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 4.3)
a(t) = 0.1886
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~81.1 % ! Maintenant le rayon est plus grand de 1/a(t) = 430 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 4.3)) / (1+0)
T(t1) = 14.44 K
La température de l'Univers était de 14.44 K (plus ~5.3 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 125A
V = (Delta lambda / lambda) x c
V = (125 / 1216) x 299792.458
V = 30 817 km/s
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (6453- 1216) / 1216
z = 4.3
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((4.3+1)^2 - 1) / ((4.3+1)^2 + 1)]
Vr = 299792.458 x (27.09/ 29.09)
Vr = 279 181 km/s [+/- 50km/s]
La distance de regard en arrière de 12.29 milliards d'années. Les photons sont partis quand l'Univers avait 1.43 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 4.3)
a(t) = 0.1886
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~81.1 % ! Maintenant le rayon est plus grand de 1/a(t) = 430 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 4.3)) / (1+0)
T(t1) = 14.44 K
La température de l'Univers était de 14.44 K (plus ~5.3 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 125A
V = (Delta lambda / lambda) x c
V = (125 / 1216) x 299792.458
V = 30 817 km/s
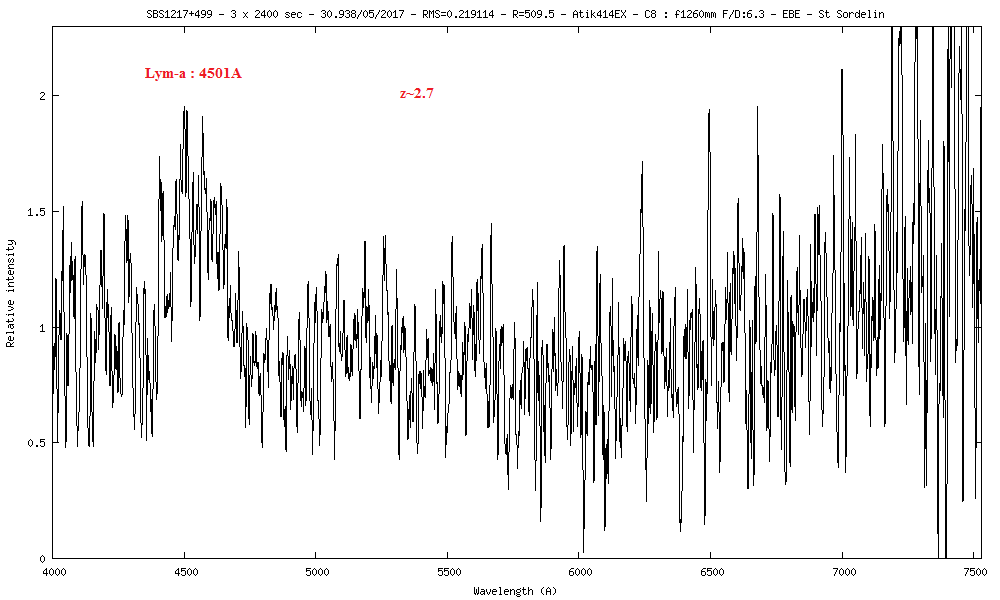
18) SBS1217+499 m=16.5 z=2.7
| _sbs1217_499_20170530_896_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Avec la raie Lyman-a à 1216A qui arrive à 6453A sur le spectre, on trouve un redshift de 4.3
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4501- 1216) / 1216
z = 2.7
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.7+1)^2 - 1) / ((2.7+1)^2 + 1)]
Vr = 299792.458 x (6.29/ 8.29)
Vr = 227 466 km/s [+/- 50km/s]
La distance de regard en arrière de 11.28 milliards d'années. Les photons sont partis quand l'Univers avait 2.43 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.7)
a(t) = 0.27
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~73 % ! Maintenant le rayon est plus grand de 1/a(t) = 270 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 2.7)) / (1+0)
T(t1) = 10.08 K
La température de l'Univers était de 10.08 K (plus ~3.69 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 83A
V = (Delta lambda / lambda) x c
V = (74.5 / 1216) x 299792.458
V = 18 367 km/s
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4501- 1216) / 1216
z = 2.7
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.7+1)^2 - 1) / ((2.7+1)^2 + 1)]
Vr = 299792.458 x (6.29/ 8.29)
Vr = 227 466 km/s [+/- 50km/s]
La distance de regard en arrière de 11.28 milliards d'années. Les photons sont partis quand l'Univers avait 2.43 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.7)
a(t) = 0.27
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~73 % ! Maintenant le rayon est plus grand de 1/a(t) = 270 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 2.7)) / (1+0)
T(t1) = 10.08 K
La température de l'Univers était de 10.08 K (plus ~3.69 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 83A
V = (Delta lambda / lambda) x c
V = (74.5 / 1216) x 299792.458
V = 18 367 km/s
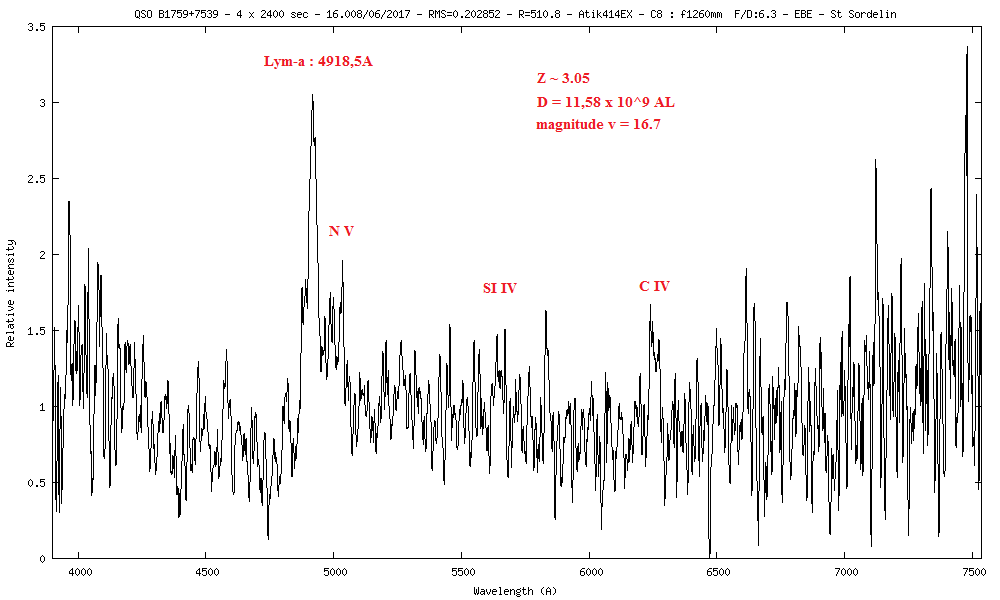
19) QSOB1759+7539 m=16.5 z=3.05
| _qso_b1759_7539_20170615_952_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Avec la raie Lyman-a à 1216A qui arrive à 6453A sur le spectre, on trouve un redshift de 4.3
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4918.5- 1216) / 1216
z = 3.045
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.045+1)^2 - 1) / ((3.045+1)^2 + 1)]
Vr = 299792.458 x (15.36/ 17.36)
Vr = 265 198 km/s [+/- 50km/s]
La distance de regard en arrière de 11.58 milliards d'années. Les photons sont partis quand l'Univers avait 2.13 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.045)
a(t) = 0.2472
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~75.3 % ! Maintenant le rayon est plus grand de 1/a(t) = 304.5 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.045)) / (1+0)
T(t1) = 11 K
La température de l'Univers était de 11 K (plus ~4 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 42A
V = (Delta lambda / lambda) x c
V = (42 / 1216) x 299792.458
V = 10 354km/s
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4918.5- 1216) / 1216
z = 3.045
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.045+1)^2 - 1) / ((3.045+1)^2 + 1)]
Vr = 299792.458 x (15.36/ 17.36)
Vr = 265 198 km/s [+/- 50km/s]
La distance de regard en arrière de 11.58 milliards d'années. Les photons sont partis quand l'Univers avait 2.13 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.045)
a(t) = 0.2472
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~75.3 % ! Maintenant le rayon est plus grand de 1/a(t) = 304.5 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.045)) / (1+0)
T(t1) = 11 K
La température de l'Univers était de 11 K (plus ~4 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de 42A
V = (Delta lambda / lambda) x c
V = (42 / 1216) x 299792.458
V = 10 354km/s
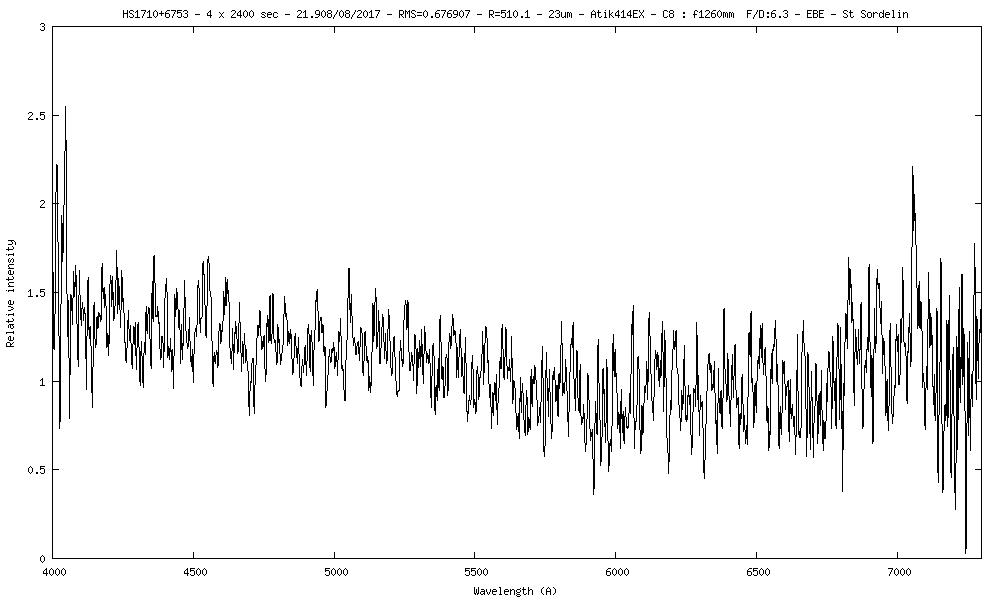
20) HS1710+6753 m=16.4 z=0.40922
| _hs1710_6753_20170821_852_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Cliquer ici pour modifier.
La raie [OIII] à 5007A qui arrive à 7056A sur le spectre,
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (7056 - 5007) / 5007
z = 0.40922
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((040922+1)^2 - 1) / ((0.40922+1)^2 + 1)]
Vr = 299792.458 x (0.9859/ 2.9859)
Vr = 98 987 km/s [+/- 50km/s]
La distance de regard en arrière de 4.4 milliards d'années. Les photons sont partis quand l'Univers avait 9.3 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 0.40922)
a(t) = 0.7096
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~29 % ! Maintenant le rayon est plus grand de 1/a(t) = 41 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 0.40922)) / (1+0)
T(t1) = 3.84 K
La température de l'Univers était de 3.8 K.
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (7056 - 5007) / 5007
z = 0.40922
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((040922+1)^2 - 1) / ((0.40922+1)^2 + 1)]
Vr = 299792.458 x (0.9859/ 2.9859)
Vr = 98 987 km/s [+/- 50km/s]
La distance de regard en arrière de 4.4 milliards d'années. Les photons sont partis quand l'Univers avait 9.3 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 0.40922)
a(t) = 0.7096
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~29 % ! Maintenant le rayon est plus grand de 1/a(t) = 41 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 0.40922)) / (1+0)
T(t1) = 3.84 K
La température de l'Univers était de 3.8 K.
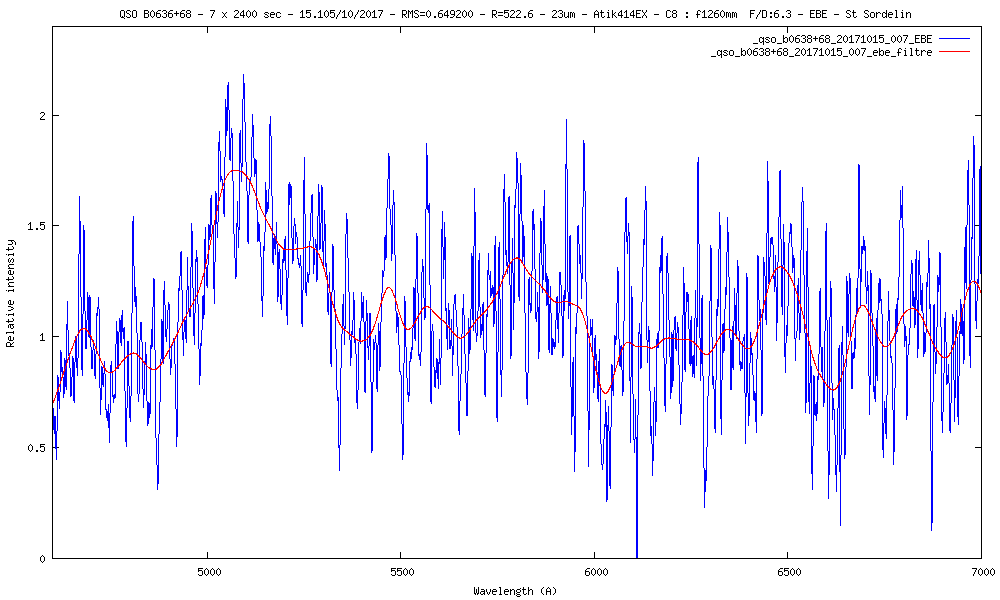
21) QSO B0636+68 m=16.46 z=3.1723
| _qso_b0638_68_20171015_007_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
| _qso_b0638_68_20171015_007_ebe_filtre.fit | |
| File Size: | 25 kb |
| File Type: | fit |
Avec la raie Lyman-a à 1216A qui arrive à 5073.5A sur le spectre, on trouve un redshift de 3.1723
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (5073.5- 1216) / 1216
z = 3.1723
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.1723+1)^2 - 1) / ((3.1723+1)^2 + 1)]
Vr = 299792.458 x (16.41/ 18.41)
Vr = 267 244 km/s [+/- 50km/s]
La distance de regard en arrière de 11.68 milliards d'années. Les photons sont partis quand l'Univers avait 2.04 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.045)
a(t) = 0.24
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~76 % ! Maintenant le rayon est plus grand de 1/a(t) = 316.6 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.1723)) / (1+0)
T(t1) = 11.37 K
La température de l'Univers était de 11.37 K (plus ~4 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de ~120A
V = (Delta lambda / lambda) x c
V = (120 / 1216) x 299792.458
V = 29 584 km/s
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (5073.5- 1216) / 1216
z = 3.1723
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.1723+1)^2 - 1) / ((3.1723+1)^2 + 1)]
Vr = 299792.458 x (16.41/ 18.41)
Vr = 267 244 km/s [+/- 50km/s]
La distance de regard en arrière de 11.68 milliards d'années. Les photons sont partis quand l'Univers avait 2.04 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.045)
a(t) = 0.24
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~76 % ! Maintenant le rayon est plus grand de 1/a(t) = 316.6 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.1723)) / (1+0)
T(t1) = 11.37 K
La température de l'Univers était de 11.37 K (plus ~4 fois la température actuelle).
La vitesse de rotation du disque d'accrétion autour du trou noir peut se mesurer avec la largeur de la raie Lyman-a à mi-hauteur (FWHM) en émission. Lyman-a a une largeur de ~120A
V = (Delta lambda / lambda) x c
V = (120 / 1216) x 299792.458
V = 29 584 km/s
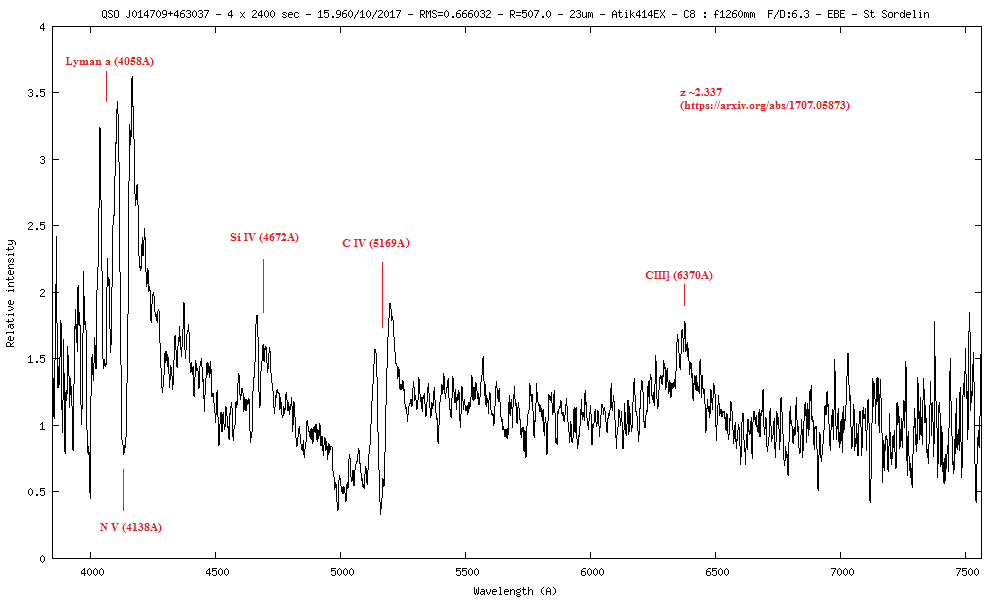
22) QSO J014709+463037 m=15.6, 15.7, 16.4, 18.1 z=2.337
| _qso14709_463037_20171015_905_ebe.fit | |
| File Size: | 43 kb |
| File Type: | fit |
Avec la raie CIII] à 1909A qui arrive à 6370A sur le spectre, on trouve un redshift de 3.1723
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (6370- 1909) / 1909
z = 2.337
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.337+1)^2 - 1) / ((2.337+1)^2 + 1)]
Vr = 299792.458 x (10.13/ 12.13)
Vr = 250 362 km/s [+/- 50km/s]
La distance de regard en arrière de 10.88 milliards d'années. Les photons sont partis quand l'Univers avait 2.83 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.337)
a(t) = 0.299
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~70 % ! Maintenant le rayon est plus grand de 1/a(t) = 234 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 2.337)) / (1+0)
T(t1) = 9 K
La température de l'Univers était de 9 K (plus ~3.3 fois la température actuelle).
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (6370- 1909) / 1909
z = 2.337
d'ou une vitesse relativiste de recession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((2.337+1)^2 - 1) / ((2.337+1)^2 + 1)]
Vr = 299792.458 x (10.13/ 12.13)
Vr = 250 362 km/s [+/- 50km/s]
La distance de regard en arrière de 10.88 milliards d'années. Les photons sont partis quand l'Univers avait 2.83 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d'echelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 2.337)
a(t) = 0.299
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~70 % ! Maintenant le rayon est plus grand de 1/a(t) = 234 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 2.337)) / (1+0)
T(t1) = 9 K
La température de l'Univers était de 9 K (plus ~3.3 fois la température actuelle).
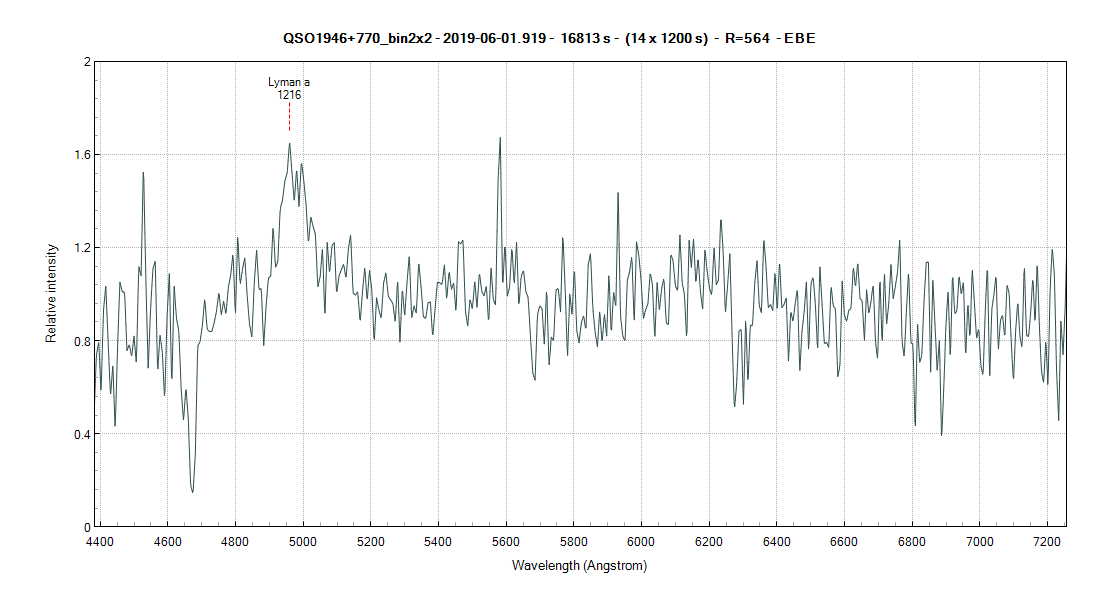
23) QSO 1946+770 m=16 z=3.096
| _qso1946_770_bin2x2_20190601_919_ebe.fit | |
| File Size: | 11 kb |
| File Type: | fit |
Avec la raie La à 1216A qui arrive à 4981A sur le spectre, on trouve un redshift de 3.096
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4960 - 1216) / 1216
z = 3.0789
d'ou une vitesse relativiste de récession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.0789+1)^2 - 1) / ((3.0789+1)^2 + 1)]
Vr = 299792.458 x (8.58/ 10.58)
Vr = 242 578 km/s [+/- 50km/s]
La distance de regard en arrière de 11.611 milliards d'années. Les photons sont partis quand l'Univers avait 2.83 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d’échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.0789)
a(t) = 0.2451
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~75.5 % ! Maintenant le rayon est plus grand de 1/a(t) = 314 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.0789)) / (1+0)
T(t1) = 11.115 K
La température de l'Univers était de 11.115K (plus ~4 fois la température actuelle).
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (4960 - 1216) / 1216
z = 3.0789
d'ou une vitesse relativiste de récession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.0789+1)^2 - 1) / ((3.0789+1)^2 + 1)]
Vr = 299792.458 x (8.58/ 10.58)
Vr = 242 578 km/s [+/- 50km/s]
La distance de regard en arrière de 11.611 milliards d'années. Les photons sont partis quand l'Univers avait 2.83 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d’échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.0789)
a(t) = 0.2451
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~75.5 % ! Maintenant le rayon est plus grand de 1/a(t) = 314 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.0789)) / (1+0)
T(t1) = 11.115 K
La température de l'Univers était de 11.115K (plus ~4 fois la température actuelle).
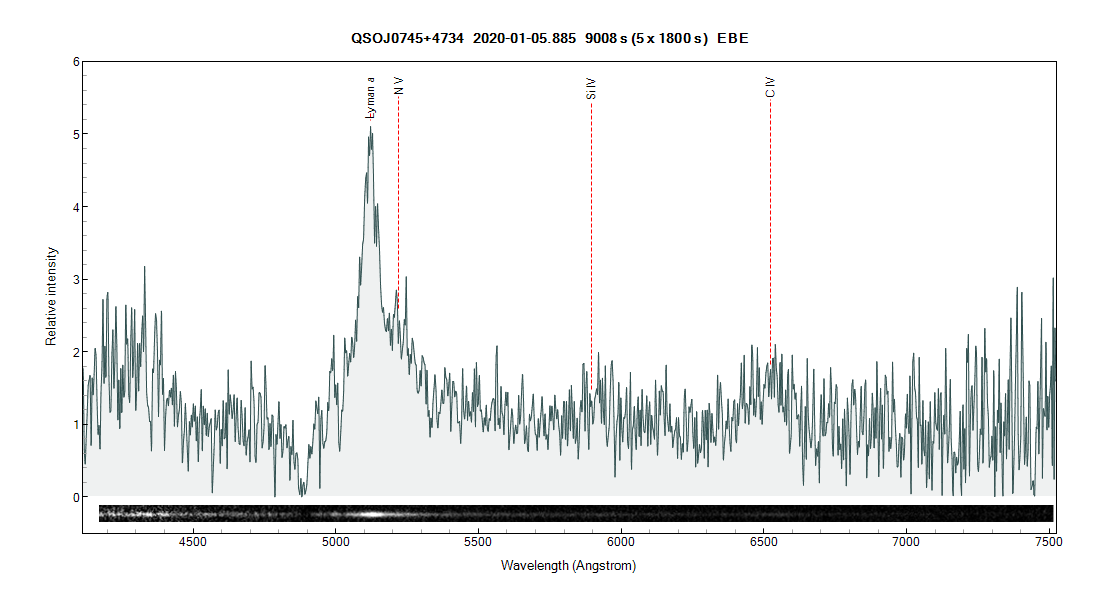
24) QSO J0745+4734 m=16.44 z=3.2119
| _qsoj0745_4734_20200105_885_ebe.fit | |
| File Size: | 23 kb |
| File Type: | fit |
Avec la raie La à 1216A qui arrive à 5121.7A sur le spectre, on trouve un redshift de 3.2119
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (5121.7 - 1216) / 1216
z = 3.2119
d'ou une vitesse relativiste de récession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.2119+1)^2 - 1) / ((3.2119+1)^2 + 1)]
Vr = 299792.458 x (16.74 / 18.74)
Vr = 267 797 km/s [+/- 50km/s]
La distance de regard en arrière de 11.709 milliards d'années. Les photons sont partis quand l'Univers avait 2.011 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d’échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.2119)
a(t) = 0.23742
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~7625 % ! Maintenant le rayon est plus grand de 1/a(t) = 321 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.0789)) / (1+0)
T(t1) = 11.47 K
La température de l'Univers était de 11.47 K (plus ~4 fois la température actuelle).
z = ((λ1 - λ0) / λ0) (λ avec en Angstrom)
z = (5121.7 - 1216) / 1216
z = 3.2119
d'ou une vitesse relativiste de récession :
Vr = c x [((z+1)^2 - 1) / ((z+1)^2 + 1)]
Vr = 299792.458 x [((3.2119+1)^2 - 1) / ((3.2119+1)^2 + 1)]
Vr = 299792.458 x (16.74 / 18.74)
Vr = 267 797 km/s [+/- 50km/s]
La distance de regard en arrière de 11.709 milliards d'années. Les photons sont partis quand l'Univers avait 2.011 milliards d'années (!!)
Avec l'expansion de l'univers cette distance (distance comobile) est maintenant réellement de 23.54 milliards d'années lumières.
Le facteur d’échelle est de :
a(t) = 1 / (1 +z)
a(t) = 1 / (1 + 3.2119)
a(t) = 0.23742
Ce qui veut dire que depuis le départ des photons l'Univers s'est agrandi de ~7625 % ! Maintenant le rayon est plus grand de 1/a(t) = 321 %
On peut aussi calculer la température de l'Univers à l'époque ou les photons sont partis grace au redshift
T(t0) / T(t1) = (1+z0) / (1+z1)
T(t0) x (1+z1) = T(t1) x (1+z0)
T(t1) = (T(t0) x (1+z1)) / (1+z0)
T(t1) = ((2,725 x (1 + 3.0789)) / (1+0)
T(t1) = 11.47 K
La température de l'Univers était de 11.47 K (plus ~4 fois la température actuelle).
25) PSS J1458+6813 m=18.37 z=4.3
| _pssj1458_6813_20200418_100_ebe.fit | |
| File Size: | 11 kb |
| File Type: | fit |
| _pssj1458_6813_20200423_917_ebe.fit | |
| File Size: | 11 kb |
| File Type: | fit |
26) PSS J1723+2243 m=18.17 z=4.53
| _pssj1723_2243_20200516_977_ebe.fit | |
| File Size: | 11 kb |
| File Type: | fit |
27) PSS J1646+5514 m=18.10 z=4.05
| _pssj1646_5514_20200518_916_ebe.fit | |
| File Size: | 14 kb |
| File Type: | fit |
Catalogue Quasars :
| quasars_pour_etienne.xlsx | |
| File Size: | 10004 kb |
| File Type: | xlsx |
Calcul de la constante de Hubble Ho :
| loi_de_hubble.ods | |
| File Size: | 121 kb |
| File Type: | ods |
Avec Ho = 75 Km/s/Mpc l'âge de l'Univers est de 12.93 milliards d'années (coefficient directeur de la pente).