Menkalinan : Eclipsing binary of Algol type
De type spectral A1IV-Vp.
Infos ici : http://sb9.astro.ulb.ac.be/DisplayFull.cgi?366+3
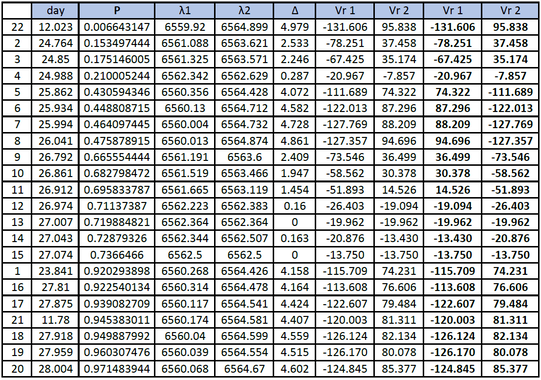
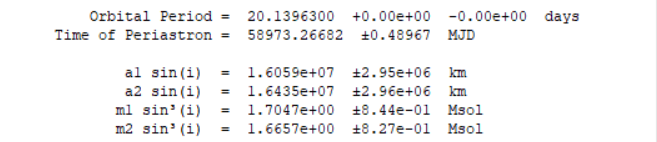
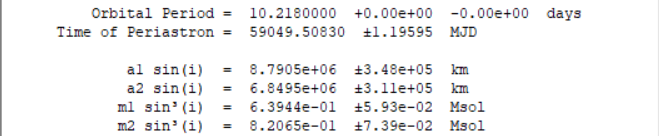
La période de cette binaire spectroscopique est de 3.96004 jours
La vitesse radiale du système s'approche de nous à 17.552 km/s
Les masses des deux étoiles sont estimées à 2.13Ms et 2.19Ms (Masse solaires)
Infos ici : http://sb9.astro.ulb.ac.be/DisplayFull.cgi?366+3
La période de cette binaire spectroscopique est de 3.96004 jours
La vitesse radiale du système s'approche de nous à 17.552 km/s
Les masses des deux étoiles sont estimées à 2.13Ms et 2.19Ms (Masse solaires)
| _menkalinan_22spectres_vhel.zip |
Le tableau des mesures des 22 spectres, classés par la période
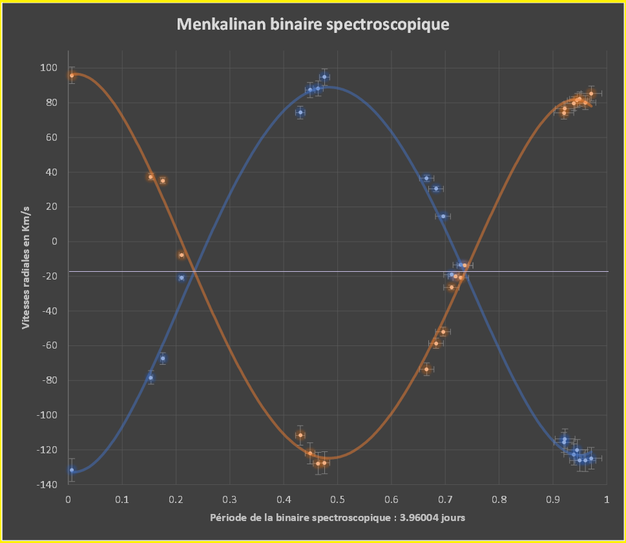
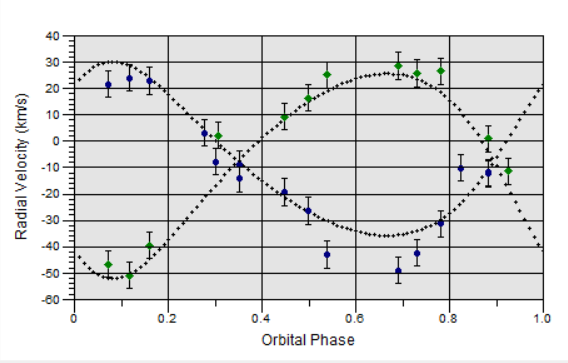
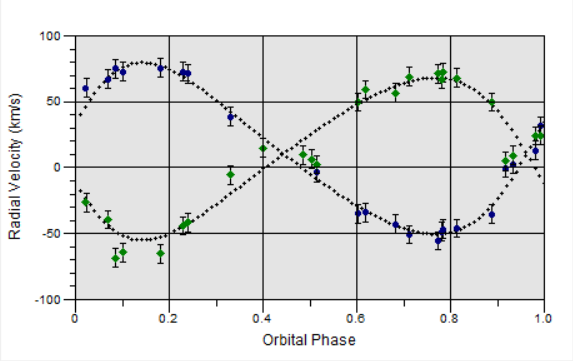
Le graph obtenu avec les mesures :
Conclusion :
Les courbes sont de parfaites sinusoïdes, donc les orbites sont circulaires et la vitesse est constante.
Les courbes possèdent la même amplitude, les deux étoiles ont donc la même masse et décrivent la même orbite.
La vitesse radiale du système : l'axe des nœuds de la sinusoïde (là ou elles se coupent) correspond à -18 km/s, donc le système binaire se rapproche de nous à -18 km/s.
La vitesse des composantes ; les amplitudes des courbes de vitesses sont les mêmes ~113 km/s. (c'est presque 4 fois plus rapide que la Terre autour du Soleil).
Séparation a en km des deux composantes :
Comme rB / rA = kB / kA
alors rA = rB
2r = k x (T / π)
Soit a = rA + rB = 113 x (3.96004 x 24 x 60 x 60) / π
Soit a = 12.3 x 10^6 km (Les deux étoiles sont proches ~1/5 de la distance Soleil-Mercure).
La masses de chaque composante : (on utilise l'unité solaire)
Donc Ma = Mb = T / (π x G) x 2 K^3
Ma = Mb = ((3.96004 x 24 x 60 x 60) / (π x 6.674 x 10^-11)) x 2 x 113 x 1000)^3
Ma = Mb = 1.632 x 10^15 x 2.886 x 10^15
Ma = Mb = 4.7 x 10^30 kg = 2.35 Ms
Les étoiles binaire se différencient des planètes autour du Soleil par le fait que :
- bien que plus massives que le Soleil
- elles sont séparées d'une distance inférieure à celle de Mercure-Soleil
Les courbes sont de parfaites sinusoïdes, donc les orbites sont circulaires et la vitesse est constante.
Les courbes possèdent la même amplitude, les deux étoiles ont donc la même masse et décrivent la même orbite.
La vitesse radiale du système : l'axe des nœuds de la sinusoïde (là ou elles se coupent) correspond à -18 km/s, donc le système binaire se rapproche de nous à -18 km/s.
La vitesse des composantes ; les amplitudes des courbes de vitesses sont les mêmes ~113 km/s. (c'est presque 4 fois plus rapide que la Terre autour du Soleil).
Séparation a en km des deux composantes :
Comme rB / rA = kB / kA
alors rA = rB
2r = k x (T / π)
Soit a = rA + rB = 113 x (3.96004 x 24 x 60 x 60) / π
Soit a = 12.3 x 10^6 km (Les deux étoiles sont proches ~1/5 de la distance Soleil-Mercure).
La masses de chaque composante : (on utilise l'unité solaire)
Donc Ma = Mb = T / (π x G) x 2 K^3
Ma = Mb = ((3.96004 x 24 x 60 x 60) / (π x 6.674 x 10^-11)) x 2 x 113 x 1000)^3
Ma = Mb = 1.632 x 10^15 x 2.886 x 10^15
Ma = Mb = 4.7 x 10^30 kg = 2.35 Ms
Les étoiles binaire se différencient des planètes autour du Soleil par le fait que :
- bien que plus massives que le Soleil
- elles sont séparées d'une distance inférieure à celle de Mercure-Soleil
ANALYSE DES DONNEES AVEC LE LOGICIEL : "SBS BINARY SPECTRO"
Menkalinan : bet Aur ; Eclipsing binary of Algol type
| menkalinan.zip |
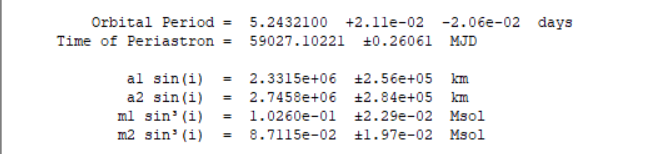
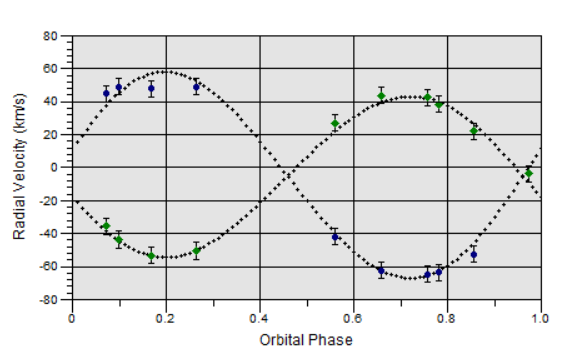
Mizar : zet01 Uma ; Spectroscopic binary
| mizar.zip |
HD160922 : ome Dra ; Spectroscopic binary
| hd160922_omedra.zip |
HD210027 : iot Peg ; Spectroscopic binary
| hd210027_iot_peg.zip |
|
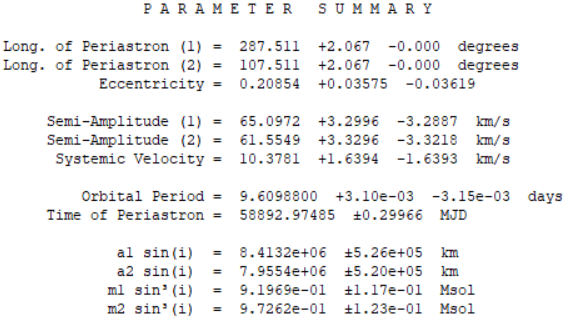
https://iopscience.iop.org/article/10.1086/131281/pdf
Masses : 1.31 +/-0.02 M sol Masses : 0.81 +/-0.01 M sol a1 : 6.75 .10^6 +/-0.03.10^6 km a2 : 10.95 .10^6 +/- 0.05.10^6 km |
HD123999 : d Boo ; Spectroscopic binary
| hd123999.zip |